![]()
![]() 定義とは、 言葉の使い方のとりきめのことである。
数学では、どのような言葉も、そのような取り決めなしで使われることはない。
(ただし、「整数」「有理数」、「和」、「積」などの言葉をきちんと定義するのは
手間がかかる。
それらについて詳細に定義するのは
この講義では控える。
(端的に言えば、整数は帰納法を援用して定義し、
有理数は整数の「商」
定義とは、 言葉の使い方のとりきめのことである。
数学では、どのような言葉も、そのような取り決めなしで使われることはない。
(ただし、「整数」「有理数」、「和」、「積」などの言葉をきちんと定義するのは
手間がかかる。
それらについて詳細に定義するのは
この講義では控える。
(端的に言えば、整数は帰納法を援用して定義し、
有理数は整数の「商」 ![]() に適当な「等しいかどうかの判定規則」と
定義する。)
それらについて詳細に定義するのは
この講義では控える。
実数は有理数の極限として
定義するのだが、今日はその「極限」の話題である。)
に適当な「等しいかどうかの判定規則」と
定義する。)
それらについて詳細に定義するのは
この講義では控える。
実数は有理数の極限として
定義するのだが、今日はその「極限」の話題である。)
![]()
![]() と
と ![]() とはなにか。
とはなにか。
は、「どんな
は、「なにかある一つの
正の整数の全体のことをこの講義では
![]() と書く。
数列とは、数学的には次のように定義できる。
と書く。
数列とは、数学的には次のように定義できる。
数列が「収束する」ということの厳密な定義をしよう。 それには、絶対値を用いる。
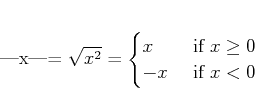
(ただし平方根は0以上のほうを選ぶ。)
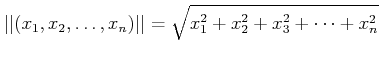
がなりたつときに言う。
この定義が使いこなせるようになれば、この講義の目標の 80% は 達せられたと言って良い。
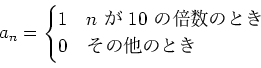
で定義するとき、
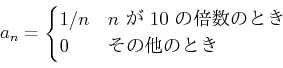
で定義するとき、