をみたす
をみたす
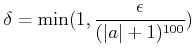
と置けば良い。 実際、このとき、
とすると
| (あ) | ||
| (い) |
| (う) |
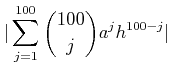 |
||
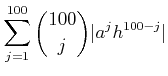 |
||
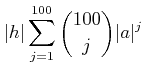 |
||
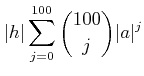 |
||
(解説)
◯
数学では二項定理のさい
![]() のような組合せの記号より
のような組合せの記号より
![]() を用いることが多い。その理由は
を用いることが多い。その理由は
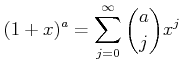
のような式を扱う際に明らかになる。
◯ 上の解答で、
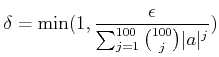
でももちろん構わない。ちょっと泥くさい感じにはなるが。
◯
単に
![]() が連続であるという事実だけならば
が連続であるという事実だけならば
を満足するような正の実数
をみたす
(解答)
(1)
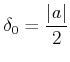
とおけば良い。じっさい、このとき
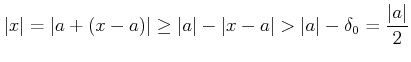
がなりたち、ゆえに
(2)
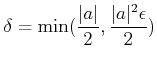
とおけばよい。 実際、このとき、
とすると
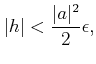 |
(い) | |
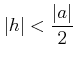 |
(ろ) |
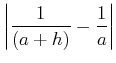 |
||
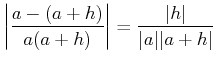 |
||
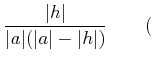 三角不等式 三角不等式 |
||
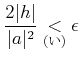 |
(解答) まず
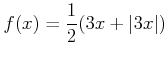
であることに注意する。
任意の正の実数 ![]() に対して、
正の実数
に対して、
正の実数 ![]() を
を
![]() で定める。
このとき、
で定める。
このとき、
![]() なる任意の
なる任意の
![]()
![]() に対して
に対して
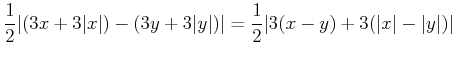 |
||
ARRAY(0x8e73c50)ARRAY(0x8e73c50)ARRAY(0x8e73c50)