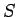 は
は 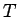 を部分集合として含む。
を部分集合として含む。
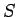 は
は 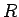 の部分環である。
の部分環である。
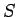 は (1),(2)を満たす最小のものである。
は (1),(2)を満たす最小のものである。
注意
「部分環」の定義により、
![]() は(
は(![]() が何であっても)
常に
が何であっても)
常に ![]() の単位元
の単位元 ![]() を元としてもつ。
しかし、単位元の存在を意識しておくために、以下では
始めから
を元としてもつ。
しかし、単位元の存在を意識しておくために、以下では
始めから ![]() には
には ![]() の単位元
の単位元 ![]() が入ったものだけを考えることにする。
が入ったものだけを考えることにする。
上の補題の証明の途中で、次の補題が必要になるので、ここに掲げておく。
もまた
実際には、生成される部分環には次のパターンのものがよく使われる。
この記法によれば、上の例の4.,5. はそれぞれ次のように書ける。
このように、
![]() が実際にはどのような元を
もつのか決定することも基本的で、重要である。それは通常
次の手順で行う。
が実際にはどのような元を
もつのか決定することも基本的で、重要である。それは通常
次の手順で行う。
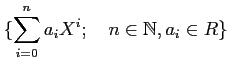
は環をなす。(足し算、かけ算は通常のものを考える。) この環を
![% latex2html id marker 1242
$\displaystyle \{\sum_{i=0}^n a_iX^i ;\quad n\in \mathbb{N}, a_i \in R\}
=\langle R\cup \{X\} \rangle_{\text{ring}}=R[X]
$](img29.png)
(したがって、これからは
注意
代数I の範囲では他に
![]()
![]()
![]() 等が重要になる。
(
等が重要になる。
(
![]() ,
,
![]() ,
,
![]() は全て体である。すなわち積は可換であり、
0
以外の各元は逆元を持つ。)
は全て体である。すなわち積は可換であり、
0
以外の各元は逆元を持つ。)
※レポート問題
(期限:次の講義の終了時まで。)