


Next: About this document ...
1=6
1 by -1
代数学 IB No.6要約
 《準同型と準同型定理》
《準同型と準同型定理》
定義 6.2
環のあいだの全単射準同型のことを、(環としての)
同型とよぶ。
容易にわかるように、
環のあいだの同型
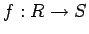
が与えられたとき、
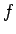
の逆写像
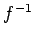
は
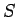
から
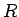
への
同型になる。
群(加法群)についての準同型の知識を使うと、次のことは直ちにわかる。
補題 6.1
環準同型 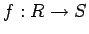 について、
について、
-
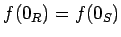 が成り立つ。
が成り立つ。
-
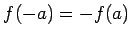 が全ての
が全ての 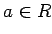 に対して成り立つ。
に対して成り立つ。
つぎに、準同型定理の説明にはいる。
定義 6.3
環準同型
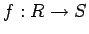
について、
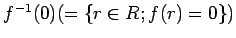
のことを、
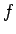
の核(Kernel)と呼び、
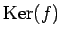
で書き表す。
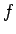 の像(Image)とは、通常通り、
の像(Image)とは、通常通り、
のことである。
補題 6.2
任意の環準同型 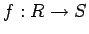 にたいして、
にたいして、
-
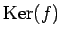 は
は 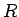 のイデアルである。
のイデアルである。
-
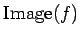 は
は 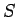 の部分環である。
の部分環である。
定理 6.1
環準同型 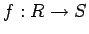 について、
について、
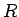 の同値関係
の同値関係 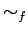 を
を
で定義し、また 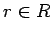 の
の
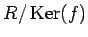 でのクラスを
でのクラスを 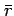 とすると、
次のことが成り立つ。
とすると、
次のことが成り立つ。
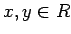 にたいして、
にたいして、
が成り立つ
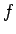 は
は
なる同型を誘導する。
代数では群、加群、環、Lie 環など、いろいろなモノについて
それぞれ「準同型定理」がなりたつが、それはすべて次の
単純な事実に基づく:

※レポート問題
つぎのうち一問を選択して解きなさい。
(期限:次の講義の終了時まで。)
- (I).
- 環の準同型
![$ f:{\mbox{${\mathbb{Z}}$}}/15{\mbox{${\mathbb{Z}}$}}\ni [a]_{15} \mapsto [a]_5\in {\mbox{${\mathbb{Z}}$}}/5{\mbox{${\mathbb{Z}}$}}$](img30.png) (
(![$ [?]_n$](img31.png) は
は 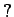 の
の
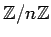 におけるクラス)
を考える。(本当は、
におけるクラス)
を考える。(本当は、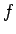 がうまく定義されていること、
さらに
がうまく定義されていること、
さらに 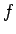 が実際に環の準同型であることを
諸君が証明すべきだが、ここではそれは要求しない。)
このとき、
が実際に環の準同型であることを
諸君が証明すべきだが、ここではそれは要求しない。)
このとき、
-
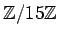 の元
の元 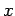 15個のそれぞれについて、
15個のそれぞれについて、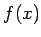 を書きなさい。
を書きなさい。
-
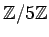 の元
の元 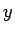 5個のそれぞれについて、
5個のそれぞれについて、
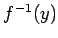 を書きなさい。
を書きなさい。
- (II).
-
![$ {\mbox{${\mathbb{Z}}$}}/11{\mbox{${\mathbb{Z}}$}}\ni [n]_{11}\mapsto [n]_5 \in{\mbox{${\mathbb{Z}}$}}/5 {\mbox{${\mathbb{Z}}$}}$](img40.png) はうまく定義されて、
環準同型になるだろうか。
はうまく定義されて、
環準同型になるだろうか。
- (III).
- 正の整数
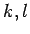 が
与えられたとき、
が
与えられたとき、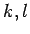 にどのような関係があれば、
にどのような関係があれば、
![$ {\mbox{${\mathbb{Z}}$}}/k{\mbox{${\mathbb{Z}}$}}\ni [n]_{k}\mapsto [n]_l \in{\mbox{${\mathbb{Z}}$}}/l {\mbox{${\mathbb{Z}}$}}$](img42.png) はうまく定義されて、
環準同型になるのか、答えなさい。
はうまく定義されて、
環準同型になるのか、答えなさい。



Next: About this document ...
2008-12-11
![]() 《準同型と準同型定理》
《準同型と準同型定理》
![]() はともに(可換とは限らない)環であるとし、
はともに(可換とは限らない)環であるとし、![]() をその間の写像とする。
このとき、
をその間の写像とする。
このとき、![]() が
が ![]() から
から ![]() への(環)準同型写像であるとは、次の条件が成り立つ
ときにいう。
への(環)準同型写像であるとは、次の条件が成り立つ
ときにいう。
![]() の像(Image)とは、通常通り、
の像(Image)とは、通常通り、
