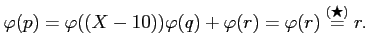ΛρΥΰΛΩΛΖΛΩΛ»ΛΙΛκΓΘΛ≥ΛΈΛ»Λ≠ΓΔ
-
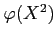 ΛρΒαΛαΛηΓΘ(≈ζΛΈΛΏΛ«ΛηΛΛΓΘ)
ΛρΒαΛαΛηΓΘ(≈ζΛΈΛΏΛ«ΛηΛΛΓΘ)
-
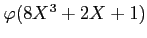 ΛρΒαΛαΛηΓΘ(≈ζΛΈΛΏΛ«ΛηΛΛΓΘ)
ΛρΒαΛαΛηΓΘ(≈ζΛΈΛΏΛ«ΛηΛΛΓΘ)
-
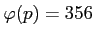 Λ»Λ Λκ
Λ»Λ Λκ
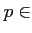
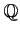
![$ [X]$](img9.png) ΛΈΈψΛρ
ΛΈΈψΛρ 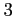 ΛΡΒσΛ≤Λ ΛΒΛΛΓΘ
ΛΩΛάΛΖΓΔΛΫΛΈΛΠΛΝΑλΛΡΛœ 3ΦΓΑ ΨεΛΈΦΑΛ«ΛΔΛκΛηΛΠΛΥΛΙΛκΛ≥Λ»ΓΘ
(≈ζΛ®Λ»ΓΔ¥ Ο±Λ ≥ΈΛΪΛαΜΜΛΈΛΏΛ«ΛηΛΛΓΘ)
ΛΡΒσΛ≤Λ ΛΒΛΛΓΘ
ΛΩΛάΛΖΓΔΛΫΛΈΛΠΛΝΑλΛΡΛœ 3ΦΓΑ ΨεΛΈΦΑΛ«ΛΔΛκΛηΛΠΛΥΛΙΛκΛ≥Λ»ΓΘ
(≈ζΛ®Λ»ΓΔ¥ Ο±Λ ≥ΈΛΪΛαΜΜΛΈΛΏΛ«ΛηΛΛΓΘ)
-
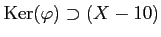
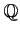
![$ [X]$](img9.png) ΛρΨΎΧάΛΖΛ ΛΒΛΛΓΘ
ΛρΨΎΧάΛΖΛ ΛΒΛΛΓΘ
-
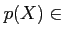
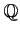
![$ [X]$](img9.png) Λρ
Λρ 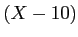 Λ«≥δΛΟΛΩΨΠΛρ
Λ«≥δΛΟΛΩΨΠΛρ 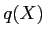 , ΆΨΛξΛρ
, ΆΨΛξΛρ 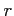 Λ»ΛΣΛ·ΓΘ
(
Λ»ΛΣΛ·ΓΘ
(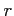 Λœ
Λœ 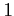 ΦΓΦΑΛ«ΛοΛΟΛΩΆΨΛξΛάΛΪΛιΓΔ 0
ΦΓΦΑΓΔΛΡΛόΛξΓΔΡξΩτ(
ΦΓΦΑΛ«ΛοΛΟΛΩΆΨΛξΛάΛΪΛιΓΔ 0
ΦΓΦΑΓΔΛΡΛόΛξΓΔΡξΩτ(
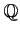 ΛΈΗΒ))
Λ≥ΛΈΛ»Λ≠
ΛΈΗΒ))
Λ≥ΛΈΛ»Λ≠ 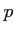 Λρ
Λρ 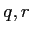 ΛρΆ―ΛΛΛΤ…ΫΛΖΛ ΛΒΛΛΓΘ(άβΧά…‘ΆΉΓΘ)
ΛρΆ―ΛΛΛΤ…ΫΛΖΛ ΛΒΛΛΓΘ(άβΧά…‘ΆΉΓΘ)
- «ΛΑ’ΛΈ
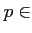
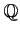
![$ [X]$](img9.png) ΛΥΛΩΛΛΛΖΛΤΓΔ
ΛΥΛΩΛΛΛΖΛΤΓΔ
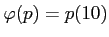 Λ§Λ ΛξΛΩΛΡΛ≥Λ»ΛρΦ®ΛΖΛ ΛΒΛΛΓΘ
Λ§Λ ΛξΛΩΛΡΛ≥Λ»ΛρΦ®ΛΖΛ ΛΒΛΛΓΘ
- ΨξΆΨ¥Ρ
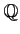
![$\displaystyle [X]/(X-10)$](img21.png)
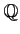
![$\displaystyle [X]
$](img22.png)
Λ«ΛΈ¬ΩΙύΦΑ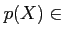
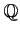
![$ [X]$](img9.png) ΛΈΞ·ΞιΞΙΛœΆ≠ΆΐΩτ
ΛΈΞ·ΞιΞΙΛœΆ≠ΆΐΩτ 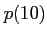 ΛΈΞ·ΞιΞΙΛ»≈υΛΖΛΛΛ≥Λ»
ΛρΦ®ΛΖΛ ΛΒΛΛΓΘ
ΛΈΞ·ΞιΞΙΛ»≈υΛΖΛΛΛ≥Λ»
ΛρΦ®ΛΖΛ ΛΒΛΛΓΘ
 Λ»ΛΛΛΠΛ≥Λ»ΛρΙ÷ΒΝΛ«άβΧάΛΖΛΩΛΈΛ«ΓΔΛΫΛΈ…τ §ΛœΚΘ≤σΛœΨΎΧάΧΒΛΖΛΥΜ»ΛΟΛΤΛβΛηΛΛΓΘ
(Μΰ¥÷ΛΥΆΨΆΒΛ§ΛΔΛλΛ–ΨΎΧάΛβΫώΛ·Λ»ΛβΛΟΛ»ΛηΛΛΛ§...)ΛΩΛάΛΖΓΔΛ…Λ≥Λ«Μ»ΛΟΛΩΛΪΛ§
ΛοΛΪΛκΛηΛΠΛ ≈ζΑΤΛΥΛΙΛκΛ≥Λ»ΓΘ
Λ»ΛΛΛΠΛ≥Λ»ΛρΙ÷ΒΝΛ«άβΧάΛΖΛΩΛΈΛ«ΓΔΛΫΛΈ…τ §ΛœΚΘ≤σΛœΨΎΧάΧΒΛΖΛΥΜ»ΛΟΛΤΛβΛηΛΛΓΘ
(Μΰ¥÷ΛΥΆΨΆΒΛ§ΛΔΛλΛ–ΨΎΧάΛβΫώΛ·Λ»ΛβΛΟΛ»ΛηΛΛΛ§...)ΛΩΛάΛΖΓΔΛ…Λ≥Λ«Μ»ΛΟΛΩΛΪΛ§
ΛοΛΪΛκΛηΛΠΛ ≈ζΑΤΛΥΛΙΛκΛ≥Λ»ΓΘ