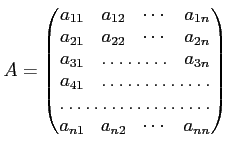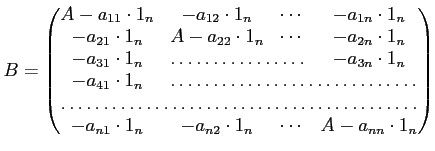Next: About this document ...
代数学演習 I 問題 No.7

例題 7.1
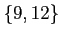
で生成される
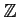
のイデアル
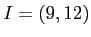
を求めよ。
解答
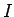 は引き算について閉じているから、
は引き算について閉じているから、
さらに、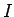 は
は
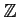 による掛け算により閉じているから、
による掛け算により閉じているから、
ところが、
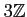 は
は 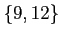 を含む
を含む
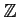 のイデアルであるから、
のイデアルであるから、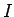 の最小性により、
の最小性により、
以上により、
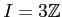 が分かった。(
が分かった。(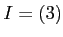 と書いても良い。次の問題も参照)
と書いても良い。次の問題も参照)
問題 7.4〜7.18 では、「環」といえば単位元を持つ可換環を指すことにします。
問題 7.4
環
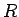
のイデアル
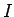
が素イデアルであるための必要十分条件は、
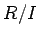
が整域であることなのを示しなさい。
問題 7.5
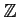
のイデアル
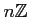
が素イデアルになるのは、
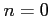
又は
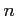
が素数のときであることを示しなさい。
問題 7.6
環
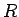
のイデアル
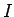
、
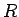
の要素
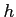
が、
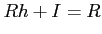
を満たすならば、
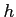
の剰余類
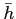
は
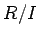
の可逆元であることを示しなさい。
問題 7.8
極大イデアルは素イデアルであることを示しなさい。
問題 7.10
![$ {\mbox{${\mathbb{Z}}$}}[X]$](img46.png)
のイデアル
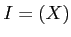
は素イデアルであって、極大イデアルではないことを示しなさい。
問題 7.11
次の
![% latex2html id marker 1833
$ {\mbox{${\mathbb{Z}}$}}[\sqrt{2}]$](img48.png)
のイデアルは素イデアルかどうか答えなさい。
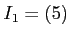
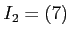
問題 7.12
環の間の準同型写像
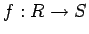
が与えられたとします。この時
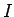
が
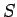
の素イデアルなら、
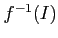
は
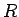
の素イデアルであることを示しなさい。
問題 7.15
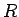
を環、
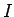
をそのイデアルとします。《
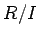
のイデアル》全体と《
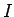
を部分集合として含む
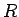
のイデアル》全体との間には一対一対応がつくことを次のようにして示しなさい。
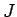 を
を 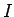 を含む
を含む 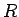 のイデアルとするとき、
のイデアルとするとき、
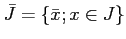
($?$ は $?$ のクラスを表す。)
は 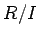 のイデアルである。
のイデアルである。
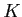 を
を 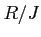 のイデアルとするとき、
のイデアルとするとき、
は 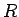 のイデアルである。
のイデアルである。
- 上の二つの対応は互いに他の逆対応になっている。すなわち、
問題 7.16
![$ {\mathbb{C}}[X]$](img26.png)
のイデアル
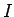
は必ずある一つの元
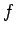
で生成される
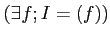
ことを示しなさい。(ヒント:
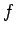
として
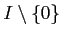
の元のうち次数が最小のものをとる。)
問題 7.17
複素数を係数に持つ多項式
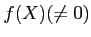
は必ず複素数の範囲で根を持つことを用いて、
![$ {\mathbb{C}}[X]$](img26.png)
の素イデアルをすべて求めよ。
問題 7.18
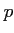
を素数とするとき、
![$ ({\mbox{${\mathbb{Z}}$}}/p{\mbox{${\mathbb{Z}}$}})[X]$](img68.png)
の元の間の次の関係式を証明しなさい。
問題 7.19
-
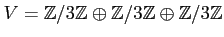 は 体
は 体
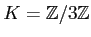 上のベクトル空間であることを示しなさい。次元はいくらですか。
上のベクトル空間であることを示しなさい。次元はいくらですか。
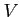 の部分群は全て
の部分群は全て 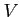 の部分ベクトル空間であることを示しなさい。
の部分ベクトル空間であることを示しなさい。
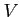 の部分群をすべて求め、それらの (
の部分群をすべて求め、それらの (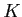 -ベクトル空間としての)次元を求めなさい。
-ベクトル空間としての)次元を求めなさい。
問題 7.20
可換環
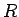
上の任意の
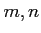
-行列
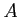
と
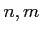
行列
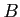
とにたいして、
が成り立つことを示しなさい。
以下の問題はかなり難しく、また後の知識が必要になる所もあるが、
あえて付け加えておいた。理論の流れが掴めればよい。
(★)式を一から証明するには、
行列式を「多重線形かつ交代的な(スカラー倍を除いて)唯一のモノ)」として特徴づける
のがもっとも自然であろう。線形代数の教科書を参照のこと。



Next: About this document ...
2008-11-14
![]()