複素数と論理(学問基礎数学コース演習) No.2

例には次のような効用がある。

• 定義自体が完全であることをチェックする。
• 相手(自分)が正しく理解するのを助ける。
• 定義に慣れる。
• 机上の空論になるのを避けることができる。
• 議論の重要な部分をより具体的に理解できる。
• 新しいアイディアを産むヒントになる。
• 正しくない議論を(反例を挙げることにより)避けることができる。

例を挙げるときには、次のことに注意すると良い。

• できるだけ単純な、誰でも理解できる例を挙げるように努力すること。
• (実験などの場合)例が再現性を持つことを確認しておくこと。
• その例が、今の議論にどのように適合するのか、説明すること。
• その例のもつ特殊事情、詳細もうまく説明できると説得力を持つ場合がある。

例題 2.1   円周率 $\pi$ を十進小数で表現したときに、"99" が現れることがあるだろうか。

$$\pi=3. 1415926535897932384626433832795028841971$$

$$6939937 \dots$$

なので、小数点以下第44位,第45位がちょうど99である。

このように相手にも分かるように、できるだけ具体的に 指摘したほうがよい。

$3$ より大きな実数は存在する。

という命題は正しいが、これは $3$ より大きな実数の存在(たとえば、$5$ ) を頭で思い浮かべているからそう思うのであって、 その 頭の中の考えを取り出して、

○ $5$ は実数であって、 $3$ より大きい

と言ったほうがよい。

前回の問題(2) でも 式だけ計算して、つまり、

$$\begin{pmatrix} a & b \\ c & d \end{... ...= \begin{pmatrix} p a + q c & p b + q d \\ r a + s c & r b + s d \end{pmatrix}$$

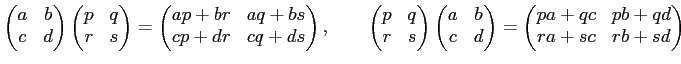
の計算だけして、両者が等しくないと即断すべきではない。 実際の両者が異るような実数 $a,b,c,d,p,q,r,s$ の例が存在することを 示すべきである。さもなければ

命題 2.1   異る実係数多変数多項式 $f(x_1,\dots,x_n),\quad g(x_1,\dots,x_n)$ にたいし、 $f(a_1,\dots,a_n)\neq g(a_1,\dots, a_n)$ なる実数 $a_1,a_2,\dots,a_n$ が存在する。

という命題を証明することになるが、これはそれなりに難しい。 実数体の代わりに、有限体の場合には命題 2.1は 実はウソなのだ。)

問題 2.1  

1. 複素数 $z,w$ が、$zw=0$ をみたしているとする。このとき、$z=0$ か $w=0$ のどちらかが成り立つことを示しなさい。
2. 2次正方行列 $A,B\in M_2($$\mbox{${\mathbb{R}}$}$$)$ が $AB=0$ をみたしているとする。このとき、 $A=0$ か $B=0$ のどちらかが成り立つと必ず言えるだろうか？

複素数についてもう少し関連する定義を書いておこう。 複素数 $z$ は、 $z=a+b J$ ($a,b$ は実数)と一意に書けたのであった。 $J$ は $J^2=-1$ を満たす「数」である。これのことを $i$ とか、 $J$ とか呼び続けてもよいのであるが、ここでは記号の節約のために 以降は $\sqrt{-1}$ と書こう。 $\sqrt{-1}$ はしばしば虚数単位と呼ばれる。

定義 2.1   複素数 $z$ について、 $z=a+b \sqrt{-1}$ ($a,b$ は実数)と書いたとき、

1. $a$ のことを $z$ の実部といい、$\Re{z}$ と書く。
2. $b$ のことを $z$ の虚部といい、$\Im{z}$ と書く。
3. $a-b \sqrt{-1}$ のことを $z$ の複素共役といい、 $\overline{z}$ と書く。

複素数は実部と虚部で与えてもいいのだが、それでは値打ちが少ない。 代わりに複素共役を使うことを考えよう。

補題 2.1   $z$ の実部と虚部は $z$ と $\overline{z}$ を用いて

$$\Re{z}=\frac{z+\overline{z}}{2},\quad \Im{z}=\frac{z-\overline{z}}{2 \sqrt{-1}}$$

と書ける。

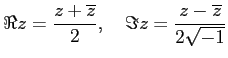
複素数の定義も思い出してみよう。

補題 2.2  

$$z= \begin{bmatrix} a & -b \\ b & a \end{bmatrix}$$

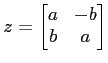
に対して、その複素共役は

$$\begin{bmatrix} a & b \\ -b & a \end{bmatrix}= \left( \begin{bmatrix} a & b \\ -b & a \end{bmatrix}\text{ の転置行列} \right)$$

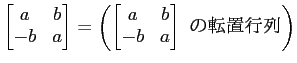
である。

転置行列に関する一般論により、つぎのことが成り立つことがわかる。

命題 2.2   任意の複素数 $z,w$ に対して、次のことが成り立つ。

1. $\overline{z+w}=\overline{z}+\overline{w}$
2. $\overline{z-w}=\overline{z}-\overline{w}$
3. $\overline{z w}=\overline{w} \overline{z}$

さらに、

命題 2.3   複素数 $z$ に対して、 $z \overline{z}$ は実数であり、 さらに $z=a+b\sqrt{-1}$ $(a,b\in$   $\mbox{${\mathbb{R}}$}$$)$ と書くと、

$$z\overline{z}=a^2+b^2 (\geq 0)$$

であることが分かる。

定義 2.2   複素数 $z$ に対して、 $z \overline{z}$ の非負の平方根 $\sqrt{z\overline{z}}$ を $z$ の絶対値と呼び、$\vert z\vert$ で書く。

$$\vert z\vert^2=\operatorname{det} \left( \begin{bmatrix} a & -b \\ b & a \end{bmatrix}\right)$$

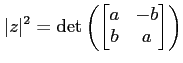
にも注意しよう。