


Next: About this document ...
複素数と論理(学問基礎数学コース演習) No.3
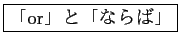 前回
前回
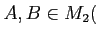
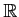
 のときや
のときや
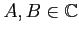 のとき、それぞれについて
のとき、それぞれについて
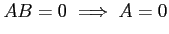
or
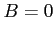
かどうか、ということについて尋ねたが、数学(に限らず、論理的な
話が必要な世界)では、言葉のアヤや「行間を読む」という曖昧さを
排除するため、
「or」と「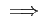 (ならば)」などのの意味はいつでも
つぎのように使うように決まっている。
(ならば)」などのの意味はいつでも
つぎのように使うように決まっている。
定義 3.1
命題 P にたいし、
その真理値は、Pが真のとき 1, P が偽のとき 0
で定める。
とくに注意が必要なのは、「P or Q」 と 「
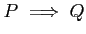 」
の使い方である。
」
の使い方である。
- 「P or Q」は、PとQ がともに正しい時もただしい。
- 「P
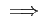 Q 」は Pが間違っていれば、Qの真偽に
かかわらず正しい。
Q 」は Pが間違っていれば、Qの真偽に
かかわらず正しい。
複素数を「数」の仲間として認めるのにさいし、
複素数の全体が、
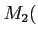
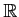
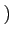 はもたない良い性質をもつということが
前回の問題でわかる。
はもたない良い性質をもつということが
前回の問題でわかる。
つぎは、複素数を視覚的に理解するという段階に進もう。
それには次のような意義がある:
- 問題を把握しやすくする。
- 問題の直観的な見方を強化し、間違いをしにくくする。
定義 3.3
平面
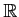
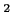
(のコピー)を一つ用意し、複素数
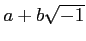
に
点
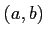
を対応させたものを
複素平面と呼ぶ
複素平面自体のことも
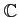 とよぶことがある。
とよぶことがある。
複素数の加法はベクトルの加法と同じだから、次のことが成り立つ。
補題 3.1
- 複素数
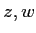 に対して、
に対して、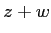 は、
は、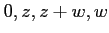 が平行四辺形になる
位置にある。
が平行四辺形になる
位置にある。
- 複素数
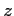 にたいして、
にたいして、 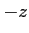 は 0
に関して
は 0
に関して 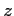 と点対称な
位置にある。
と点対称な
位置にある。
複素数の乗法はどうだろうか、完全な答えは来週与えることにして、
今週は次の補題と問題をやって頂こう。
問題 3.1
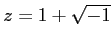
にたいし、
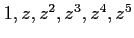
を複素平面上にプロットした図を描いてみよ。
2009-01-21
![]() 前回
前回
![]()
![]()
![]() のときや
のときや
![]() のとき、それぞれについて
のとき、それぞれについて
![]() 」
の使い方である。
」
の使い方である。
![]()
![]()
![]() はもたない良い性質をもつということが
前回の問題でわかる。
はもたない良い性質をもつということが
前回の問題でわかる。