-
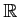
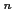 の開集合
の開集合 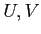 の共通部分
の共通部分 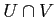 は開集合であることを示しなさい。
は開集合であることを示しなさい。
-
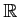
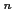 の開集合
の開集合 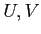 の和集合
の和集合 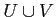 は開集合であることを示しなさい。
は開集合であることを示しなさい。
-
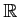
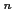 の無限個の開集合
の無限個の開集合
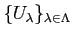 の和集合
の和集合
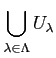
は開集合であることを示しなさい。
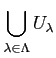
は開集合であることを示しなさい。
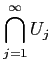
が開集合ではない例を挙げなさい。
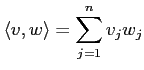
で定義する。 このとき、
を示しなさい。
が成り立つことを前小問を使って示しなさい。(三角不等式)
今回の以下の問題は、連続性の定義は ![]() -
-![]() 論法を用いて行い、
それを用いて解答すること。すなわち、
論法を用いて行い、
それを用いて解答すること。すなわち、![]() が
が ![]() で
連続であるとは、
で
連続であるとは、
で定義することにする。単に「連続」といえば、「定義域の各点で連続」の意味である。
は連続であることを示しなさい。
が成り立つことを示しなさい。
は連続であることを示しなさい。
は連続であることを示しなさい。
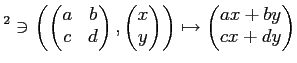
は連続であることを示しなさい。
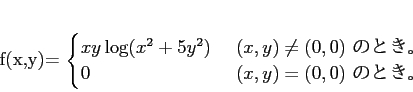
で定義する。この
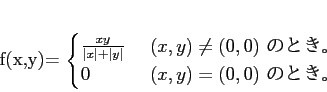
で定義する。この