


Next: About this document ...
解析学 IA演習 No.5
問題 5.1
について、
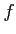
の
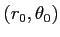
における微分
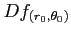
と
その行列式
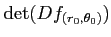
を求めよ。
問題 5.2
について、
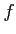
の
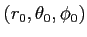
に
おける微分
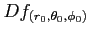
と
その行列式
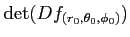
を求めよ。
問題 5.3 (各1)
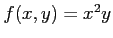
にたいして、
-
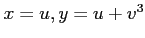 とおいて、
とおいて、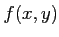 を
を 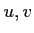 で書き表しなさい。
それを
で書き表しなさい。
それを 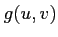 とおく。すなわち、
とおく。すなわち、
- 偏導関数
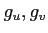 をそれぞれ求めよ。
をそれぞれ求めよ。
- 微分の連鎖律
をこの場合に確かめなさい。
問題 5.4 (各1)
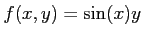
にたいして、問題
5.3 の(2) と (3) を繰り返しなさい。
二変数 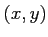 の関数
の関数 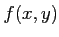 に関する偏微分方程式
に関する偏微分方程式
は、「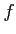 は
は 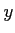 を止めて
を止めて 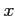 を動かしたときに定数である」
ということを意味しているから、その一般解は、
を動かしたときに定数である」
ということを意味しているから、その一般解は、
(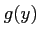 は「任意の」一変数関数)
というかたちで与えられる。以下の問題はこれを踏まえて答えること。
は「任意の」一変数関数)
というかたちで与えられる。以下の問題はこれを踏まえて答えること。
問題 5.5 (各1)
二変数
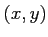
の関数
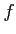
に関する偏微分方程式
を解きたい。
-
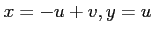 と変数変換して、上記方程式を
と変数変換して、上記方程式を
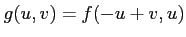 に
関する方程式に書き直しなさい。
に
関する方程式に書き直しなさい。
- この偏微分方程式の一般解を求めなさい。
問題 5.6
二変数
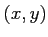
の関数
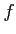
に関する偏微分方程式
を解きなさい。(ヒント:
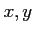
を適当に一次変換してみよ。)
問題 5.7
三変数
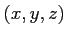
の関数
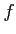
に関する偏微分方程式
を解きなさい。
問題 5.8 (配った問題は間違っていたので、欠番)



Next: About this document ...
2009-05-28
![]() の関数
の関数 ![]() に関する偏微分方程式
に関する偏微分方程式