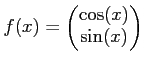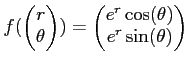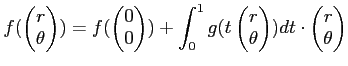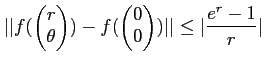Next: About this document ...
解析学 IA演習 No.6
問題 6.2
二変数関数
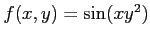
にたいして、
二階偏導関数
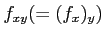
,
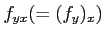
をそれぞれもとめよ。
補題 6.1 (絶対積分評価)
閉区間上の(ベクトル値)関数
が区分的に連続(すなわち、![$ [a,b]$](img29.png) の有限分割が存在してそのそれぞれの区間で連続)
であるとき、
の有限分割が存在してそのそれぞれの区間で連続)
であるとき、
問題 6.4 (各1)
- 定数関数
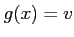 に対して上の補題を証明しなさい。
に対して上の補題を証明しなさい。
-
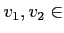
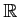
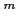 と
と
![$ a_1\in [a,b]$](img34.png) が与えられていて、
が与えられていて、
で定まるような関数 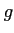 に対して、上の補題を証明しなさい。
に対して、上の補題を証明しなさい。
- 一般の
区分的に定数であるような関数に対して、上の補題を証明しなさい。
一般の区分的に連続な関数については、
上の問題の極限として補題が証明される。
以下の問題では、とくに断らない限り、絶対積分評価を用いて良い。



Next: About this document ...
2009-05-27
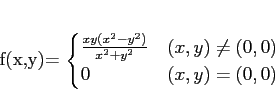
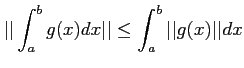
![\begin{displaymath}
g(x)=
\begin{cases}
v_1 &\text{ if }x \in [a,a_1] \\
v_2 &\text{ if }x \in (a_1,b]
\end{cases}\end{displaymath}](img35.png)