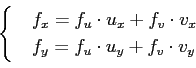 |
(※) |
もっと正確に書くと、上の式は
の意味である。 同様にして、
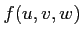 (
(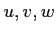 は2変数
は2変数 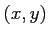 の関数)
の関数)
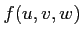 (
(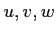 は3変数
は3変数 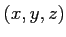 の関数)
の関数)
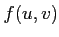 (
(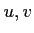 は3変数
は3変数 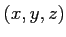 の関数)
の関数)
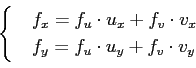 |
(※) |
の
を
の
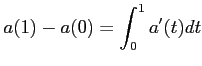
の
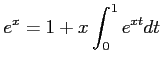
を示しなさい。
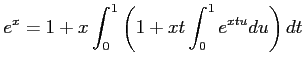
であることを示し、ついで
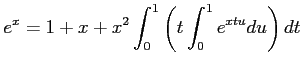
を示しなさい。
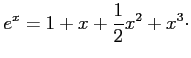 (三度積分を行った式)
(三度積分を行った式)
の形の式を得なさい。
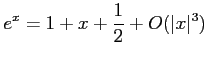
を示しなさい。
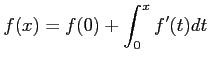
を
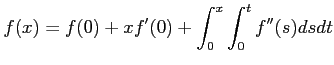
を示しなさい。
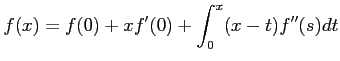
を示しなさい。
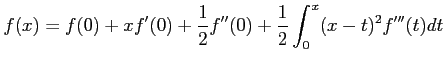 |
(T2) |
一般の ![]() に対しては
に対しては
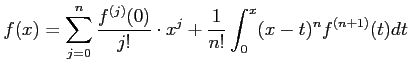 |
(Tn) |
に対して、
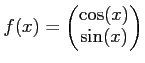
に
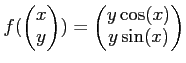
にたいして、
をみたすベクトル
をみたすベクトル
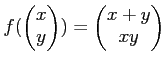
に対して繰り返しなさい。 (前問よりやさしいが、それゆえかえって戸惑うかも知れない。) なお、「剰余項」は積分で出さなくても良い。
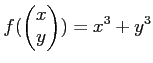
に対して繰り返しなさい。
に対して、