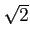 の近似値
の近似値 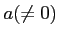 にたいし、
にたいし、
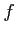 の
の 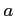 での接線
での接線 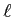 の方程式を求め、
の方程式を求め、 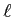 と
と 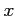 軸との
交点の
軸との
交点の 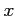 座標を
座標を 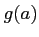 と置こう。
と置こう。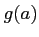 を具体的に
を具体的に 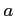 の式で書きなさい。
の式で書きなさい。
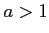 ならば
ならば 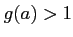 かつ
かつ
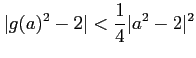
であることを示しなさい。-
![$ a\in [1,4]$](img13.png) ならば
ならば
![$ g(a) \in [1,4]$](img14.png) かつ
かつ
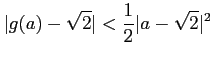
であることを示しなさい。 -
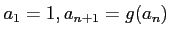 の最初の数項と、
その小数展開(意味のある桁までで良い。)を求めなさい。
((1)-(3) が解けたあとにとくこと。)
の最初の数項と、
その小数展開(意味のある桁までで良い。)を求めなさい。
((1)-(3) が解けたあとにとくこと。)
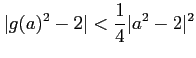
であることを示しなさい。
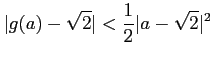
であることを示しなさい。
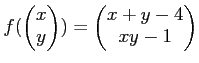
について、
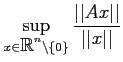
を求めなさい。