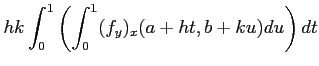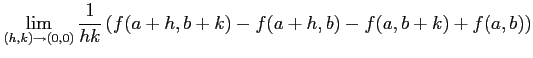Next: About this document ...
解析学 IA演習 No.9
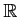
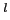 上の共通の定義域を持つ(実数値もしくはベクトル値)
関数
上の共通の定義域を持つ(実数値もしくはベクトル値)
関数 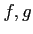 が与えられているとする。
ラグランジュの未定乗数法は、
が与えられているとする。
ラグランジュの未定乗数法は、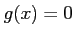 を満たすような
を満たすような 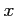 のうちで
のうちで
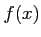 の停留値を議論するのに使われる。
の停留値を議論するのに使われる。
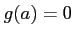 なる
なる 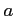 で
で 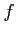 が停留するとしよう。
が停留するとしよう。
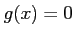 を満たす
を満たす 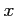 の全体は
の全体は
なる空間(接線ならぬ「接線形多様体」)で近似される。この空間上 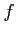 が停留するということは、
が停留するということは、
ということである。前問よりこれは
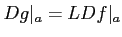 をみたす行列
をみたす行列 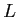 が存在することと同値である。行列
が存在することと同値である。行列 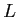 を「未定乗数」としてあらたな
変数に組み込むのが素晴しいアイディアである。
が、理論は二の次である。(だったら書くな。)
未定乗数法の最大の良さはその使い勝手の良さにある。以下の数問を参照。
を「未定乗数」としてあらたな
変数に組み込むのが素晴しいアイディアである。
が、理論は二の次である。(だったら書くな。)
未定乗数法の最大の良さはその使い勝手の良さにある。以下の数問を参照。
問題 9.3 (実)
二次曲線
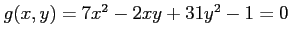
上の点のうち、
原点からもっとも近い点ともっとも遠い点をそれぞれ求めなさい。
(ヒント: 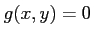 なる条件下で
なる条件下で 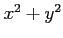 の停留条件を
未定乗数法で求めよ。)
の停留条件を
未定乗数法で求めよ。)
問題 9.4
実二次曲線
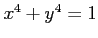
について、前問を繰り返しなさい。
問題 9.5
実二次曲線
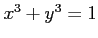
について、前問を繰り返しなさい。
(距離最小の点は存在するが、最大の点は...)
問題 9.6
条件
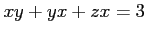
,
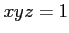
を満たす
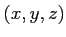
のなかで、
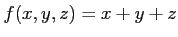
の値の
停留値を見たい。そこで
を考えて、
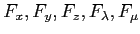
の共通零点をもとめ、
続いて
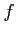
の与条件下での停留点および停留値をもとめよ。
問題 9.8 (全部で1)
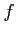
は二変数の
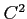
級関数と仮定する。このとき、
- 等式
と絶対積分評価を用いて、
を示しなさい。
-
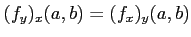 を示しなさい。
を示しなさい。
問題 9.9
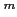
の開集合
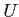
上定義された
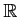
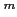
-値
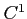
関数
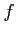
と
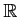
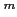
の開集合
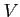
上定義された
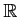
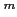
-値連続関数
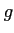
が与えられていて、
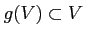
かつ
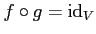
がなりたっていたとする。
このとき、もし、点
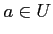
で
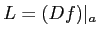
が行列として可逆(つまり、
逆行列を持つ。言い換えると、
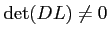
)だったとすると、
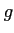
は
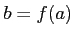
において微分可能であって、
がなりたつことを示しなさい。
(ヒント:
がなりたつことを示せば良い。
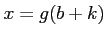 とおけば、
とおけば、
あとは 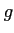 の連続性に着目すれば良い。)
の連続性に着目すれば良い。)



Next: About this document ...
2009-07-29
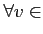
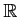
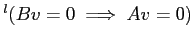 .
.
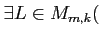
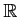
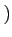 があって、
があって、 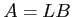 がなりたつ。
がなりたつ。
![]()
![]() 上の共通の定義域を持つ(実数値もしくはベクトル値)
関数
上の共通の定義域を持つ(実数値もしくはベクトル値)
関数 ![]() が与えられているとする。
ラグランジュの未定乗数法は、
が与えられているとする。
ラグランジュの未定乗数法は、![]() を満たすような
を満たすような ![]() のうちで
のうちで
![]() の停留値を議論するのに使われる。
の停留値を議論するのに使われる。
![]() なる
なる ![]() で
で ![]() が停留するとしよう。
が停留するとしよう。
![]() を満たす
を満たす ![]() の全体は
の全体は