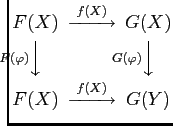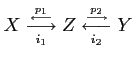Next: Bibliography
Categories, abelian categories and cohomologies.
Yoshifumi Tsuchimoto

Our treatment here is a (rather strange) mixture of [2],[1]
DEFINITION 03.1
Let
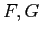
be two functors from a category
to a category
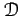
.
A morphism of functros from
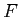
to
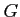
is a family of morphisms in
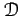
:
one for each
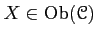
, satisfying the following condition: for any morphism
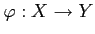
in
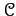
, the diagram
is commutative.
DEFINITION 03.2
Let
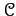
be a category,
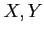
be objects of
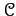
.
Then an morphism
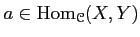
is an
isomorphism in
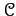
if there exists
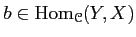
such that the relations
hold.
Objects
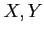
in a category
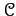
are said to be
isomorphic
if there exists at least one isomorphism between them.
Note that by combining the above two definitions, we obtain a definition
of a notion of isomorphisms of functors.
DEFINITION 03.3
A functior
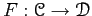
is said to be an
equivalene of category
if there exists a functor
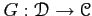
such that the
functor
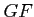
is isomorphic to
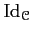
, and the functor
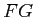
is
isomorphic to
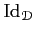
.
If such a thing exists, we say that the two categories are
equivalent.
DEFINITION 03.5
An category
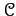
is an
additive category
if it satisfies the following axioms:
- A1.
- Any set
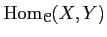 is an additive group.
The composition of morphisms is bi-additive.
is an additive group.
The composition of morphisms is bi-additive.
- A2.
- There exists a null object
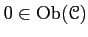 .
.
- A3.
- For any objects
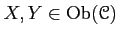 , there exists a biproduct
of
, there exists a biproduct
of 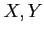 . Namely, there exists a diagram
. Namely, there exists a diagram
in
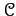 such that
such that
holds.
DEFINITION 03.6
Let
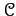
be a category,
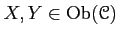
, adn
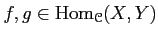
.
An
equalizer 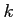
of
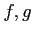
is
an arrow
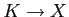
in
which satisfies the
following properties:
-
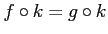 .
.
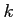 is ``universal'' amoung morphisms which satisfies (1).
In other words, if
is ``universal'' amoung morphisms which satisfies (1).
In other words, if 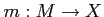 is a morphism in
is a morphism in
 such that
such that
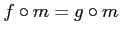 , then there exists a unique arrow
, then there exists a unique arrow 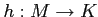 in
in
 which satisfy
which satisfy
By reversing the directions of arrows above, one may define the notion of
coequalizers
DEFINITION 03.7
Let
be an additive category. Then the equalizer
(respectively, coequalizer) of an arrow
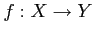
and
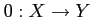
is called the
kernel
(respectively,
cokernel) of
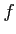
.
DEFINITION 03.8
An additive category
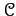
is said to be
abelian if it satisfies the
following axioms.
- A4-1.
- Every morphism
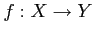 in
in
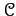 has a kernel
has a kernel
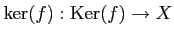 .
.
- A4-2.
- Every morphism
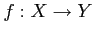 in
in
 has a
cokernel
has a
cokernel
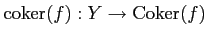 .
.
- A4-3.
- For any given morphism
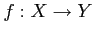 , we have
a suitably defined isomorphism
, we have
a suitably defined isomorphism
in
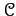 .
More precisely,
.
More precisely, 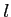 is a morphism which is defined by the following relations:
is a morphism which is defined by the following relations:



Next: Bibliography
2009-05-15
![]()