Yoshifumi Tsuchimoto
![]() We first review definition and some basic properties of modules.
We first review definition and some basic properties of modules.
such that the following properties hold.
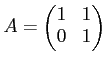
over
Then:
A cochain complex in an abelian category
![]() is a sequence of objects
and morphisms in
is a sequence of objects
and morphisms in
![]()
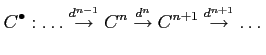
such that
Cohomology objects of the cochain complex are