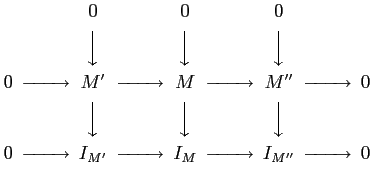-
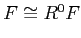 .
.
- For each short exact sequence
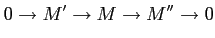
and for each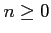 there is a natural homomorphism
there is a natural homomorphism
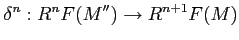
such that we obtain a long exact sequence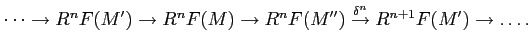
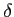 is natural. That means, for a morphism of short exact sequences
is natural. That means, for a morphism of short exact sequences
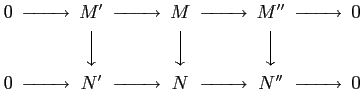
the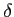 's give a commutative diagram:
's give a commutative diagram:
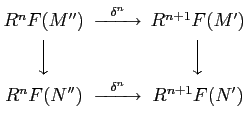
- For each injective objective object
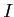 of
of 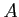 and for each
and for each 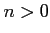 we have
we have 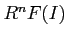 .
.