Yoshifumi Tsuchimoto
where in the above notation
Let ![]() be a ring,
be a ring,
![]() be a ring homomorphism such that
be a ring homomorphism such that
![]() is invertible in
is invertible in ![]() for any
for any ![]() .
Then there exists a unique ring homomorphism
.
Then there exists a unique ring homomorphism
![]() such that
such that
holds.
Then (1)
(2)
![]() is multiplicatively closed.
is multiplicatively closed.
(3) We have
(4)
![]() is injective.
is injective.
where the equivalence relation
We may introduce a ![]() -module structure on
-module structure on ![]() in
an obvious manner.
in
an obvious manner.
![]() thus constructed satisfies an universality condition which
the reader may easily guess.
thus constructed satisfies an universality condition which
the reader may easily guess.
We may also localize categories, but we need to deal with non commutativity of composition. To simplify the situation we only deal with a localization with some nice properties as follows:
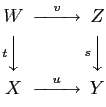
commutes.
In a simpler (but not rigorous) words,
for each ``composable ![]() '', there exists
'', there exists ![]() such
such
![]() .
Similarly, for each composable
.
Similarly, for each composable ![]() , there exists
, there exists ![]() such
that
such
that
![]() holds.
holds.