![]()
![]() 定義とは、 言葉の使い方のとりきめのことである。
数学では、どのような言葉も、そのような取り決めなしで使われることはない。
(ただし、「整数」「有理数」、「和」、「積」などの言葉をきちんと定義するのは
手間がかかる。
それらについて詳細に定義するのは
この講義では控える。
(端的に言えば、整数は帰納法を援用して定義し、
有理数は整数の「商」
定義とは、 言葉の使い方のとりきめのことである。
数学では、どのような言葉も、そのような取り決めなしで使われることはない。
(ただし、「整数」「有理数」、「和」、「積」などの言葉をきちんと定義するのは
手間がかかる。
それらについて詳細に定義するのは
この講義では控える。
(端的に言えば、整数は帰納法を援用して定義し、
有理数は整数の「商」 ![]() に適当な「等しいかどうかの判定規則」と
定義する。)
それらについて詳細に定義するのは
この講義では控える。
実数は有理数の極限として
定義するのだが、今日はその「極限」の話題である。)
に適当な「等しいかどうかの判定規則」と
定義する。)
それらについて詳細に定義するのは
この講義では控える。
実数は有理数の極限として
定義するのだが、今日はその「極限」の話題である。)
![]()
![]() と
と ![]() とはなにか。
とはなにか。
は、「どんな
は、「なにかある一つの
正の整数の全体のことをこの講義では
![]() と書く。
数列とは、数学的には次のように定義できる。
と書く。
数列とは、数学的には次のように定義できる。
数列が「収束する」ということの厳密な定義をしよう。 それには、絶対値を用いる。
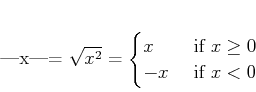
(ただし平方根は0以上のほうを選ぶ。)
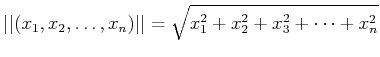
次の三角不等式も実は高次元の場合にも成り立つ。
がなりたつ。
いよいよ収束性の定義を述べよう。
がなりたつときに言う。
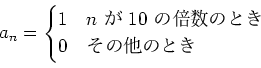
で定義するとき、
(証明) 背理法で、![]() がある数
がある数 ![]() に収束したとする。
収束の定義の
に収束したとする。
収束の定義の ![]() として
として
![]() を採用しよう。
ある
を採用しよう。
ある ![]() が存在して、
が存在して、
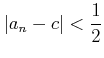 |
(※) |
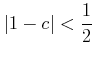
がわかり、
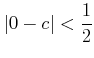
がわかる。
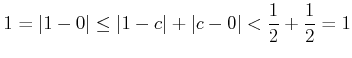
となって矛盾である。
よって、![]() はいかなる値にも収束しない。
はいかなる値にも収束しない。
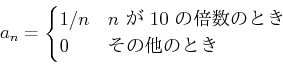
で定義するとき、
(証明)
与えられた
![]()
![]()
![]() にたいして、
にたいして、
![]() として、
として、
![]() より大きい整数を一つとっておく。
(そのようなもの(すなわち与えられた実数よりも大きな整数)
が存在することは、「アルキメデスの原理」として
保証されているが、マアさしあたっては当り前だと思っても良い。)
より大きい整数を一つとっておく。
(そのようなもの(すなわち与えられた実数よりも大きな整数)
が存在することは、「アルキメデスの原理」として
保証されているが、マアさしあたっては当り前だと思っても良い。)
この ![]() が収束の定義の
が収束の定義の ![]() の役割を果たすことを示そう。
実際、
の役割を果たすことを示そう。
実際、 ![]() なる任意の
なる任意の ![]() にたいして、
にたいして、
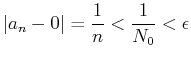
となって、いずれの場合にせよ
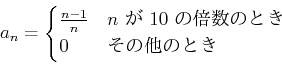
で定義するとき、