


Next: About this document ...
微分積分学概論AI要約 No.3
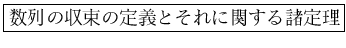
収束の定義は前回の定義 2.4で述べた通りである。
それでは定義 2.4 の判定法を満たす 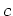 は唯一つだろうか?
は唯一つだろうか?
定理 3.1
数列
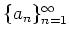
が(ある人が確かめたところ)
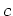
に収束し、
(別の人が確かめたところ)
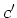
にも収束するなら、
である。つまり、数列の収束先は存在するとしたら唯一つしかない。
そこで、つぎのように定義することができる。
定義 3.2
数列
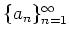
がある数
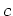
に収束するとき、
と書いて、
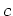
のことを
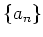
の
極限と呼ぶ。
定理 3.3 (``定理1.2'')
-
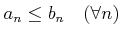 で、かつ
で、かつ 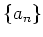 ,
, 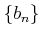 が
収束するなら、
が
収束するなら、
-
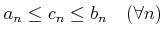 で、かつ
で、かつ 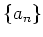 ,
, 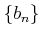 が
同じ数
が
同じ数 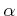 に収束するなら、
に収束するなら、 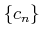 も
も 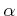 に収束する。
に収束する。
定理 3.4 (``定理1.3'')
収束する数列は有界である。
定理 3.5 (``定理1.4'')
実数列
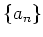
,
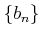
はそれぞれ収束するとする。このとき、
- 「極限をとる」という操作は線形である。すなわち、
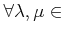
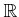 に対して
に対して
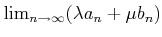 は収束して、
は収束して、
- 「実数の乗法は連続である。」
- 実数の除法は「連続」である。 もっと詳しく言うと、
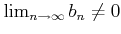 なら、
有限個の例外を除いて
なら、
有限個の例外を除いて 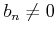 であって、
であって、
定義 3.6
実数列
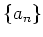
が
単調増加であるとは、
がなりたつときにいう。
次の定理は、
既知の数から未知の数 (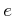 など) を作り出すときに有効である。
など) を作り出すときに有効である。
定理 3.7 (``定理1.5'')
上に有界な単調増加数列は収束する。
問題 3.1
実数列
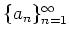
が
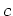
に収束するとき、
は収束すると言えるだろうか。言えるならばその収束先と理由を、言えないならば
反例を作りなさい。
(注意: 今回の講義で証明する定理をただ用いるのではなく、
収束の定義に戻って (
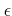
-
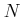
論法で)説明すること。)



Next: About this document ...
2009-04-24
![]()
![]() は唯一つだろうか?
は唯一つだろうか?
![]() など) を作り出すときに有効である。
など) を作り出すときに有効である。