


Next: About this document ...
微分積分学概論AI要約 No.4

定理 4.1 (テキスト``定理1.4'')
実数列
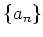
,
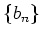
はそれぞれ収束するとする。このとき、
- 「極限をとる」という操作は線形である。すなわち、
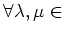
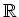 に対して
に対して
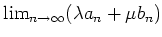 は収束して、
は収束して、
- 「実数の乗法は連続である。」
- 実数の除法は「連続」である。 もっと詳しく言うと、
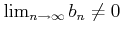 なら、
有限個の例外を除いて
なら、
有限個の例外を除いて 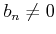 であって、
であって、
定義 4.2
実数列
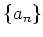
が
単調増加であるとは、
がなりたつときにいう。
次の定理は、既知の数から未知の数 (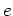 など) を作り出すときに有効である。
など) を作り出すときに有効である。
定理 4.3 (テキスト``定理1.5'')
上に有界な単調増加数列
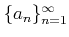
はその上限に収束する。
もちろん、「上」を全て「下」に、「単調増加」を
単調減少に置き換えた命題も成り立つ。
問題 4.1
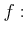
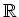
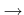
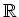
を
で定義する。
さらに、
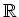
の部分集合
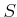
を
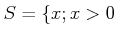
かつ
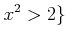
で定義する。
このとき、
- 任意の
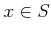 に対して、
に対して、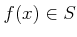 がなりたつことを示しなさい。
がなりたつことを示しなさい。
- 任意の
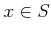 に対して、
に対して、
が成り立つことを示しなさい。
- 実数列
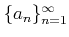 を
を
で定義すると、この数列はある実数 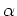 に収束することを
示しなさい。
に収束することを
示しなさい。
- 実数
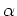 は
は
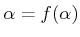 を満たすことを示しなさい。
を満たすことを示しなさい。
上の数列は大変早く収束する。
余力のある人は、電卓や数式処理ソフトなどで、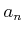 の
最初の数項を計算してみると良い。
の
最初の数項を計算してみると良い。

2009-05-08
![]()
![]() など) を作り出すときに有効である。
など) を作り出すときに有効である。
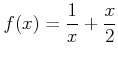
![]() の
最初の数項を計算してみると良い。
の
最初の数項を計算してみると良い。
