![]() まず二項定理について復習しておこう。
まず二項定理について復習しておこう。
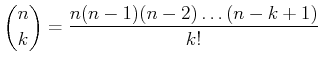
のことを、二項係数とよぶ。
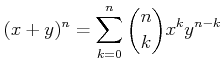
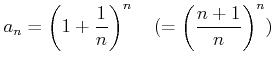
とおく。このとき
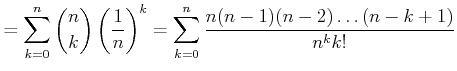 |
||
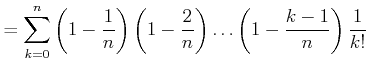 |
![]()
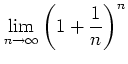
のことを
命題 5.3 の和は大変早く収束する。
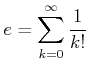
の部分和のところで線を入れること。 上の和のうちどの程度までを気にする必要があるだろうか? (楽しんでやること)
講義とレポート採点が終わったあとから気づいた注意: 上の書き方では誤解を招きますね。「等式
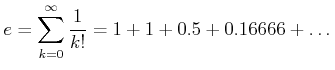
において、右辺の和がそれぞれどの割合で寄与しているか その様子を帯グラフで書け。但しグラフの長さは(定規ではかれる範囲で 正確に)