微分積分学概論AI要約 No.8

今回から、関数の話に話題の重点をうつす。

これから、 「$a$ の近くで定義されている(実数値)関数 $f$ 」 という言い方をもちいることがある。これは、 次の二つの状況を同時に満足していることを 言い表す言葉である。

1. $f$ は $\mbox{${\mathbb{R}}$}$ のある部分集合 $S$ 上定義されている関数 ( $f: S\to$   $\mbox{${\mathbb{R}}$}$ )である。
2. $S$ は $a$ を含むある開区間 $I$ を部分集合として含む

定義 8.1 ( ``1.3.2'' )  

$f$ は実数 $a$ の近くで定義された関数であるとする。このとき、 $x$ が $a$ に近づくときの $f(x)$ の極限値 は $A$ である (「$x\to a$ のとき $f$ は $A$ に収束する」とも言う) とは、

$$\forall \epsilon>0, \exists \delta>0; ( 0<\vert x-a\vert<\delta \implies \vert f(x)-A\vert<\epsilon)$$

が満たされるときに言う。

($x\to a$ の過程において、「$x=a$ を許さない」というのが 一つのポイントである。これは、

$$\lim_{x\to a}\frac{\sin(x)-\sin(a)}{x-a}=\cos(a)$$

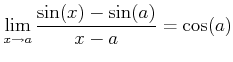
のような不定形の極限を相手にすることが多いからである。 )

補題 8.2   上の定義の状況のもとで、関数 $f(x)$ の $x$ が $a$ に近づくときの極限値は 存在するとすれば唯一つである。

定義 8.3   $f(x)$ の $x\to a$ の極限を(それがもし存在すれば、)

$$\lim_{x\to a} f(x)$$

とかく。

定義 8.4 ( ``1.3.3'' )  

$f$ は実数 $a$ の近くで定義された関数であるとする。このとき、 $x$ が $a$ に近づくときの $f(x)$ の右極限値 は $A$ である (「 $x\downarrow a$ のとき $f$ は $A$ に収束する」とも言う) とは、

$$\forall \epsilon>0, \exists \delta>0; ( 0<x-a<\delta \implies \vert f(x)-A\vert<\epsilon)$$

が満たされるときに言う。$f$ および $a$ が与えられたとき、右極限値が もし存在すれば一意的である。これを

$$\lim_{x\downarrow a} f(x)$$    あるいは $$\lim_{x\to a+0} f(x)$$

と書く。左極限値も同様に定義される。

問題 8.1  

$$\lim_{x\to 2} x^3$$

はいくらか。(結果が正しいことを極限の定義に基づいて証明せよ。)

前回、「アクションプラン」と題して何か喋りましたが、 それは、この間のアンケートの結果を踏まえたもので、 その要点は:

1. 講義の最初の5分間ぐらいを解説タイムに当てます。
2. 講義の分からないところ、考え方で良く分からないところなどを レポートに具体的に書いて「これについて解説タイムで解説して欲しい」 という風に要望して頂ければできる限りお答えします。
3. その他、下のような「ツボ」を要約に載せるようにします。

◎ いつになったら

$a_n=\frac{1}{n}$ という数列を考えよう。 意訳すれば、コビトサンが一日に一度数字を作ってくれていると考えれば良い。

$$a_1=1$$ 1日目 

$$a_2=0.5$$ 2日目 

$$a_3=0.33333\dots$$ 3日目 

$$a_4=0.25$$ 4日目 

$$a_5=0.2$$ 5日目 

$$a_6=0.1666\dots$$ 6日目 

$$a_7=0.14285714\dots$$ 7日目 

いつになったら $a_n$ の値は $0.01$ より小さくなるだろうか。

答は101日目。

いつになったら $a_n$ の値は $0.001$ より小さくなるだろうか。

答は1001日目。

いつになったら $a_n$ の値は $0.000234$ より小さくなるだろうか。

(ちょっと考えて)答は4274日目。

いちいち聞かれていては面倒だ。記号を用いて自動化しよう。

いつになったら $a_n$ の値は $\epsilon(>0)$ より小さくなるだろうか。

答は $\lceil 1/\epsilon \rceil$ ( $1/\epsilon$ より大きい最小の整数)日目。

同様に、いつになったら

$$\frac{12 n^2 +25 n +2009} { n^2 +6 n +8}$$

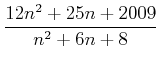
と $12$ との差は $0.1$ 以下になるだろう。

◎「論理的な計算」を理解するために

(a)表には数、裏にはアルファベットの書かれたカードが4枚ある。 それらは A, K, 4, 7 であった。 それらのカードのことごとくが 「母音の裏側の数字は必ず偶数になっている」 というルールを満足していることを確かめるためには、 最低で何枚のカードをめくる必要があるか。(それらはどのカードか。)

(b)4人のヒトがいる。

• ビールを飲んでいるヒト(年齢不詳。)
• お茶を飲んでいるヒト(年齢不詳。)
• 何かを飲んでいる24歳の青年。
• 何かを飲んでいる16歳の生徒。

それらのヒトのことごとくが 「20歳未満はアルコールを飲んではイケナイ」 というルールを満足していることを確かめるためには、 最低で何人のヒトについて新たな情報を得る必要があるか。 (それらはどのヒトか。)

詳細は「偶数」「母音」でネットを検索すると良い。 どちらの問題が分かりやすいだろうか。(爆問学問 File-071より)

◎レポートの解答から

◯ 問題6.2 では、$\{a_n\}$ が有界であることを証明するのが ポイントである。 「$\{a_n\}$ が有界として」 とか 「$\{a_n\}$ が有界と仮定する」で解答が始まるのはのっけからオカシイ。

◯ $\{a_n\}$ が $c$ に収束するということを縮めて $\lim_{n\to \infty} a_n$ と書くのである。 $\{a_n\}$ は 「$\{a_n\}$ が $c$ に収束するので、 $\lim_{n\to \infty} a_n =c$ 」 などと書くのは、全く理解しないという印象を与える。

◯ 収束列が単調とは限らない。 例えば $(-1)^n \frac{1}{n}$ は 0 に 収束するし、 $5+(-1)^n \frac{1}{n}$ は $5$ に収束する。

◯ 「数列が有界である」とは $\{a_n\}$ 全体が ある区間 $[N,N']$ に すっぽりと入ることを意味している。 一つ一つの元が有界であるからといって、全体が有界であるとは限らない。