


Next: About this document ...
微分積分学概論AI要約 No.10

定義 10.1
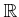
の部分集合
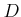
上で定義された
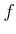
が
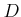
で連続であるとは、その定義域の全ての点
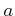
で連続であること、すなわち、
が成り立つときに言う。
上の定義は、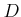 が開区間や閉区間に限らず、一般的に
適用できる形で述べられている。詳しくは多変数の場合に譲ろう。
が開区間や閉区間に限らず、一般的に
適用できる形で述べられている。詳しくは多変数の場合に譲ろう。
時間の都合で述べるのは省略するが、極限についても同様のことがらが
成り立つ。教科書定理1.10を参照のこと。
上の定理は、下の定理の多変数版を用いるともっと鮮やかに証明される
定理 10.4
二つの連続関数の合成関数は連続である。
定理 10.5 (``教科書定理1.13'')
関数
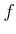
が
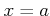
で連続とし、
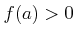
とする。このとき、
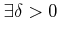
で、
を満たすものが存在する。
次のことは、「連続 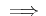 グラフがつながっている」ということの
表現法の一つと言える。
グラフがつながっている」ということの
表現法の一つと言える。
定理 10.6 (``教科書定理1.14'', 中間値の定理)
関数
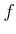
が閉区間
![$ [a,b]$](img21.png)
で連続(すなわち、
![$ [a,b]$](img21.png)
の各点で連続)とする。
このとき
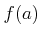
と
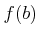
の中間の値
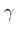
にたいして、

をみたすような
![$ c\in [a,b]$](img26.png)
が存在する。
上の定理は、位相空間論において「連結集合の連続像は連結である」という
定理に一般化される。
(区間は実数直線の連結部分集合として特徴づけることができる。)
問題 10.1
とおくと、
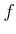
は
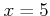
において連続であることを定理9.2の(☆)にしたがって
(つまり、今回の定理達を用いずに)
証明しなさい。
問題 10.2
とおくと、
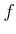
は
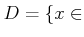
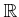
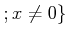
において連続であることを
定義にしたがって
証明しなさい。
問題8.1 解答。
である。これを示そう。
任意の
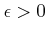 にたいして、
にたいして、
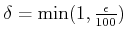 とおく。
すると、
とおく。
すると、
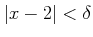 を満たすような 任意の
を満たすような 任意の 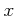 に対して、
に対して、
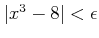 となることを以下に示そう。
簡単のため、
となることを以下に示そう。
簡単のため、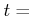
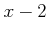 で定まる新しい変数
で定まる新しい変数 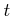 をもちいて、
をもちいて、
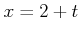 と変数変換することにする。
と変数変換することにする。
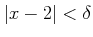 により、
により、
-
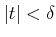
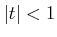
が成り立つことに注意する。
がなりたつ。
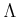
解説: 今回は文字で表されるような数 (
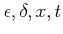 など)の
扱い方に
注目しよう。
など)の
扱い方に
注目しよう。
以上を元に、上の証明の、4つの下波線部分を見てみる。
- 正の数
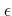 が与えられている。数学で「任意」という場合には
『どんな値が来ても以下の議論は大丈夫である。』という意味である。
したがって、
が与えられている。数学で「任意」という場合には
『どんな値が来ても以下の議論は大丈夫である。』という意味である。
したがって、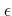 の値を証明するヒトの都合によって変更したりすることは
できない。
の値を証明するヒトの都合によって変更したりすることは
できない。
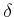 の値を決めている。この値は証明のなかで既に決まっているデータ
(今の場合は
の値を決めている。この値は証明のなかで既に決まっているデータ
(今の場合は 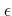 ) が決まった途端に確実に決まる。
) が決まった途端に確実に決まる。
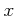 が登場した。これは 決められた範囲
が登場した。これは 決められた範囲
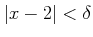 を動き回る。
それ以外には
『どんな値が来ても以下の議論は大丈夫である』ように以下の議論を組み立てる
必要がある。
を動き回る。
それ以外には
『どんな値が来ても以下の議論は大丈夫である』ように以下の議論を組み立てる
必要がある。
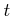 は計算の便のための、いわば脇役である。
その値は
は計算の便のための、いわば脇役である。
その値は 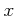 の値から確実に決まる。
の値から確実に決まる。
ARRAY(0x8e5ae10)



Next: About this document ...
2009-06-22
![]()
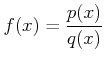 ($p,q$ は $x$ の多項式)
($p,q$ は $x$ の多項式)
![]() グラフがつながっている」ということの
表現法の一つと言える。
グラフがつながっている」ということの
表現法の一つと言える。
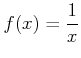
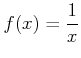
![]() にたいして、
にたいして、
![]() とおく。
すると、
とおく。
すると、
![]() を満たすような 任意の
を満たすような 任意の ![]() に対して、
に対して、
![]() となることを以下に示そう。
簡単のため、
となることを以下に示そう。
簡単のため、![]()
![]() で定まる新しい変数
で定まる新しい変数 ![]() をもちいて、
をもちいて、
![]() と変数変換することにする。
と変数変換することにする。
![]() により、
により、
![]() など)の
扱い方に
注目しよう。
など)の
扱い方に
注目しよう。