


Next: About this document ...
微分積分学概論AI要約 No.11

定義 11.1 (``1.3.6'')
実数のある区間
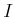
で定義された関数
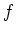
が狭義単調増加関数であるとは、
をみたすときにいう。
定理 11.2 (``教科書定理1.16'')
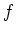
が閉区間
![$ [a,b]$](img5.png)
上の狭義単調増加な連続関数であれば、
の逆関数
が存在する。
さらに、この
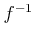
は連続で、かつ狭義単調増加である。
例 11.3
正の整数
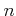
に対して、
0
以上の実数を定義域とする関数
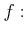
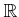
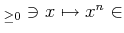
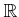
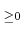
は連続であり、狭義単調増加である。この関数は全射でもあるから、
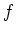
は逆写像を持つ。この関数を
と書く。
つまり
![% latex2html id marker 1021
$ y=\sqrt[n]{x}$](img15.png)
は
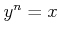
を満たす唯一の正の実数である。
命題 11.4
任意の正の実数
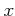
に対して、
がなりたつ。
Proof.
![% latex2html id marker 1037
$ y=\sqrt[n]{x}$](img20.png)
とおくと、定義により、
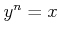
.
ゆえに、
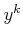
は
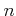
乗して
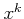
になる実数である。
そのような実数は唯一つ、すなわち
![% latex2html id marker 1049
$ \sqrt[n]{x^k}$](img24.png)
しかないのであるから、
両者は等しい。
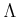
同様にして、次のことが分かる。
命題 11.5
正の整数
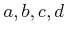
が
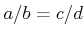
を満たせば、任意の実数
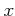
にたいして、
がなりたつ。
この命題がなりたつので、
![% latex2html id marker 1064
$ \sqrt[b]{x^a}$](img28.png) のことを
のことを
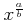 と
書いても誤解の恐れがない。
と
書いても誤解の恐れがない。
例 11.6
この例では、高校で習う三角関数の知識は
既知であるとする。
-
![$ [-\frac{\pi}{2},\frac{\pi}{2}] \ni x\mapsto \sin(x) \in [-1,1]$](img30.png) は狭義単調増加連続関数である。その逆関数のことを
は狭義単調増加連続関数である。その逆関数のことを
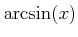 と書く。
と書く。
-
![$ [0,\pi] \ni x\mapsto \cos(x) \in [-1,1]$](img32.png) は狭義単調減少連続関数である。その逆関数のことを
は狭義単調減少連続関数である。その逆関数のことを
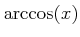 と書く。
と書く。
-
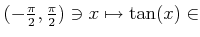
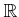 は狭義単調増加連続関数である。その逆関数のことを
は狭義単調増加連続関数である。その逆関数のことを
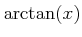 と書く。
と書く。
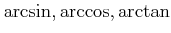 はそれぞれ
はそれぞれ
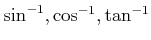 などと書くこともある。
などと書くこともある。
問題 11.1
正の整数
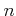
にたいし、
![% latex2html id marker 1097
$ a_n=\sqrt[n]{2}$](img38.png)
とおく。
このとき、数列
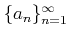
は
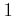
に収束することを
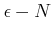
法を用いて証明しなさい。
(レポート問題が二問以上ある時はどちらか一方を解けばよい。)
問題9.1 解答。
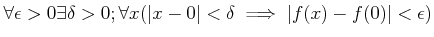 |
(☆) |
の否定、すなわち
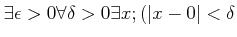 and and 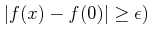 |
(★) |
を示せば良い。
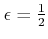 と定める。
どんな
と定める。
どんな 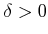 をとってきても、
をとってきても、
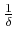 より大きな整数
より大きな整数 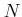 が存在する
(アルキメデスの原理)。
が存在する
(アルキメデスの原理)。
この 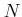 にたいし、
にたいし、
とおけば、
なのに、
で、とくに
である。
上の状況をゲームで表現することができる。
(★) において、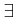 記号のついている変数を「味方側」の変数、
記号のついている変数を「味方側」の変数、
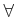 記号のついているほうを「敵側」の変数と見ることにしよう。
味方側の変数はこちらで決めれれば良い(決めるべきである)のにたいし、
敵側の変数はこちらから決めることはできない。
結論
記号のついているほうを「敵側」の変数と見ることにしよう。
味方側の変数はこちらで決めれれば良い(決めるべきである)のにたいし、
敵側の変数はこちらから決めることはできない。
結論
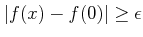 が最終的に成立することを「味方の勝ち」
と呼べば、
上の証明は味方が必勝である(ような味方の戦略がある)ことを表している。
が最終的に成立することを「味方の勝ち」
と呼べば、
上の証明は味方が必勝である(ような味方の戦略がある)ことを表している。
結論
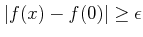 .
.
こちらは 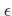 として
として
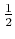 を選択した。対する敵側
を選択した。対する敵側
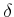 は意外な一手。これを見たわたしは
は意外な一手。これを見たわたしは 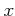 を慎重に選び、
勝利に結びつけたのであった。
を慎重に選び、
勝利に結びつけたのであった。
|
(★)の攻守を入れ換えた(敵側から眺めた)ものが(☆)である。
例えば
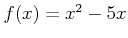 の
の 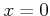 における連続性をしめすのは、以下のようなゲーム戦略を考えているのと同じである。
における連続性をしめすのは、以下のようなゲーム戦略を考えているのと同じである。
結論
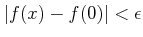 .
.
敵側 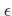 は意外な一手。対するこちらはそれを見て
冷静に
は意外な一手。対するこちらはそれを見て
冷静に 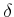 を選択。これが必殺の一撃であった。
以下は敵側
を選択。これが必殺の一撃であった。
以下は敵側 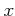 をいろいろと試みて反撃するも、後の祭りであった。
をいろいろと試みて反撃するも、後の祭りであった。
|
上を見ても分かるように、(☆),(★)はそれぞれ次のように言い換えても良い。
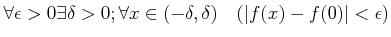 |
(☆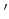 )
) |
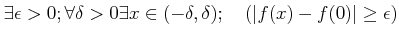 |
(★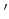 )
) |



Next: About this document ...
2009-07-07
![]()
![]() と定める。
どんな
と定める。
どんな ![]() をとってきても、
をとってきても、
![]() より大きな整数
より大きな整数 ![]() が存在する
(アルキメデスの原理)。
が存在する
(アルキメデスの原理)。
![]() にたいし、
にたいし、
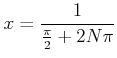
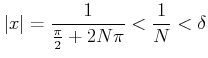
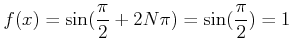
![]() 記号のついている変数を「味方側」の変数、
記号のついている変数を「味方側」の変数、
![]() 記号のついているほうを「敵側」の変数と見ることにしよう。
味方側の変数はこちらで決めれれば良い(決めるべきである)のにたいし、
敵側の変数はこちらから決めることはできない。
結論
記号のついているほうを「敵側」の変数と見ることにしよう。
味方側の変数はこちらで決めれれば良い(決めるべきである)のにたいし、
敵側の変数はこちらから決めることはできない。
結論
![]() が最終的に成立することを「味方の勝ち」
と呼べば、
上の証明は味方が必勝である(ような味方の戦略がある)ことを表している。
が最終的に成立することを「味方の勝ち」
と呼べば、
上の証明は味方が必勝である(ような味方の戦略がある)ことを表している。
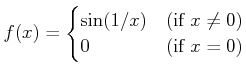
![]() の
の ![]() における連続性をしめすのは、以下のようなゲーム戦略を考えているのと同じである。
における連続性をしめすのは、以下のようなゲーム戦略を考えているのと同じである。