![]()
は
![]()
定義 5.5 の ![]() を思い出しておこう。
を思い出しておこう。
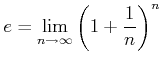
逆関数の定理により、![]() は
は ![]() の単調増加連続関数であることが
わかる。
の単調増加連続関数であることが
わかる。
数学では断らない限り対数の底としては ![]() をとり、
自然対数を考えるのが普通である。
をとり、
自然対数を考えるのが普通である。
上の定理は ![]() の
の ![]() の挙動を記述するものだが、
の挙動を記述するものだが、
![]() のときの挙動も大事である。
のときの挙動も大事である。
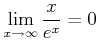
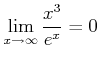
を証明せよ。(この講義でいままでに得た知識、定理の中のどれを用いても 構わない。)
問題10.2 解答。
![]()
![]()
![]() において
において ![]() が連続であることを示そう。
任意の
が連続であることを示そう。
任意の
![]() にたいして、
にたいして、
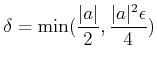
とおく。
![]() なる任意の
なる任意の ![]() に対して、
に対して、
![]() がなりたつことを示そう。
そのために、
がなりたつことを示そう。
そのために、![]() とおく。一方で、
とおく。一方で、![]() であり、
他方で
であり、
他方で
![]() から、
から、
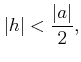 かつ かつ |
(*) | |
 |
(**) |
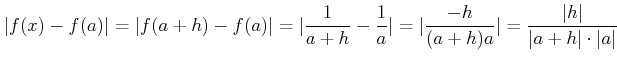 |
(A) |
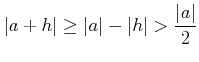
であって、 なおかつ正の数の分数においては、分母が大きくなるほどその値は 小さくなるから、
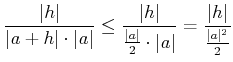 |
(B) |
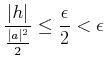 |
(C) |
である。
(A),(B),(C)をつなぎあわせると、めでたく
(任意の
![]() に対して、
に対して、![]() を上のように定めれば
を上のように定めれば
![]() なる任意の
なる任意の ![]() に対して)
に対して)
がなりたつことがわかった。
注意
上の解答で用いた三角不等式は、講義で述べたもの
| (△) |
を得る。あとは適当に移項すれば良い。不等式の向きに注意。 うろ覚えで間違えた不等式を書かないように、とくに始めの間は 基本の三角不等式(△)をしっかり覚えてあとはそれを上のように 応用することを考えた方が良い。