微分積分学概論AI要約 No.13

三角関数を 数学的に厳密に定義するためには、もうすこし準備を要する。 具体的には、角度、線分の長さ、面積の具体的な定義や、べき級数の 取り扱い等である。 ただ、これらの関数を全く知らないでいると不便なので、 ある程度厳密性を犠牲にして以下では概略を述べる。 高校までにならったことを思い出しておくとよい。

定義 13.1   $x$ -$y$ 平面の単位円 $C:x^2+y^2=1$ を考える。 $x$ 軸の正の部分と角度 $\theta$ だけ進んだ半直線 $\ell$ と $C$ との交点 $P$ の $x$ 座標を $\cos(x)$ , $y$ 座標を $\sin(x)$ と 書く。

注意点: 角度は(とくに断らない限り)常に弧度法を用いる。

定義から、次の式がなりたつ。

$$(\sin(x))^2+(\cos(x))^2=1.$$

定理 13.2  

$$\lim_{x\to 0} \frac{\sin(x)}{x}=1$$

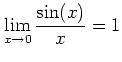
(三角関数の微分の基本になる式)

三角関数、指数関数、対数関数の微分は、前回および今回の「基本になる式」と 次のような加法公式(乗法公式)をもちいて計算される。

定理 13.3   任意の実数 $x,y$ について次の式がなりたつ。

1. $e^{x+y}=e^x e^y.$
2. $\sin(x+y)=\sin(x)\cos(y)+\cos(x)\sin(y)$
3. $\cos(x+y)=\cos(x)\cos(y)-\sin(x)\sin(y)$

また、任意の正の実数 $x,y$ にたいして

$$\log(x y)=\log(x)+\log(y)$$

がなりたつ。

問題 13.1  

$$\lim_{x\to 0} \cos(x)=1$$

を(できれば今回の諸定理と $\epsilon$ -$\delta$ 論法で)証明しなさい。 ただし、 $\vert x\vert < \frac{\pi}{2}$ ならば $\cos(x)>0$ であることは 自由に用いて良いことにする。

問題11.1 解答。

任意の $\epsilon>0$ にたいして、 $1/\epsilon$ より大きい整数 $N$ をとってくる。 (アルキメデスの原理により、そのような整数は存在する。) $n>N$ なる任意の $n$ にたいして、

$$(1+\epsilon)^n\geq (1+n \epsilon) > 1+ N \epsilon>1+1 =2.$$

$\sqrt[n]{\bullet}$ の単調性により、この範囲の $n$ にたいして、

$$1+ \epsilon >\sqrt[n]{2} >\sqrt[n]{1}=1$$

よって、($n>N$ なる $n$ にたいして) $\vert\sqrt[n]{2}-1\vert \leq \epsilon$ である。

解説 $\{a_n\}$ の最初の数項を実際に小数で数値計算している答案も見受けられた。 そのような試みも大変有意義であると思う。コンピュータの数式処理ソフトで 計算してみると、最初の5項は次のようになる。

$$a_1=2, \quad a_2=1.4142.., \quad a_3=1.2599..,\quad a_4=1.1892..,\quad a_5=1.14869..$$

では、コンピュータが使えない場合はどのように計算すれば良いだろうか。 例えば、 $a_5=\sqrt[5]{2}$ はどのように計算すれば良いだろうか。 区間縮小法を用いてみよう。(すると逆関数の定理の「ココロ」がわかる。)

$$1^5 =1 < 2< 2^5=32 1 2 1.5$$

$$1^5=1 < 2< 1.5^5=7.59.. 1 1.5 1.25$$

$$1^5=1 < 1.25^5=3.05.. 1 1.25 1.125$$

$$1.125^5=1.80..< 2<1.25^5=3.05.. 1.125 1.25 1.1875$$

$$1.125^5=1.80..<2< 1.1875^5=2.36.. 1.125 1.1875 1.15625$$

$$1.125^5=1.80<2< 1.15625^5=2.066.. \implies 1.125 <\sqrt[5]{2}<1.15625$$

遅いけれども着実に $\sqrt[5]{2}$ の値がしぼられていくことが見てとれるだろう。

問題11.2 解答。 こちらは難問であった。(ア)と (イ)の二つのステップに分ける。

(ア) まず

   $$\mbox{${\mathbb{Q}}$}$$$$\ni q\mapsto 2^q \in$$   $$\mbox{${\mathbb{R}}$}$$

が単調増加であることを示そう。 $q_1,q_2\in$   $\mbox{${\mathbb{Q}}$}$ が $q_1<q_2$ をみたすとき、 $q_1,q_2$ の共通分母であるような整数 $b(>0)$ をとって、

$$a_1,a_2,b\in {\mbox{${\mathbb{Z}}$}}, \quad q_1=\frac{a_1}{b},\quad q_2=\frac{a_2}{b},\quad a_1 <a_2$$

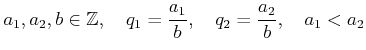
とできる。 $2^{a_1} < 2^{a_2}$ は定義によりすぐに確かめられる。$b$ 乗根をとるという操作 ( $x\mapsto \sqrt[b]{x}$ という関数)は 単調であるから、

$$\sqrt[b]{2^{a_1}} <\sqrt[b]{2^{a_2}}$$

すなわち $2^{q_1}<2^{q_2}$ がわかる。

(イ)本題に移ろう。任意の $\epsilon>0$ にたいして、 $1/\epsilon$ より 大なる整数 $N$ をとり、 $\delta=1/N$ とおく。(とりかたにより、 自動的に $\delta \leq 1$ がなりたつことと、 $\delta\in$   $\mbox{${\mathbb{Q}}$}$ であることがわかる。) 11.1 の解答と同様にして、

$$1< 2^\delta \leq 1+\delta$$

がわかる。両辺の逆数をとって、 $1-\delta < (1+\delta )^{-1}$ に注意すると

$$1-\delta < (1+\delta)^{-1}< 2^{-\delta} < 1.$$

$q\mapsto 2^q$ の単調性(ア)により、 $-\delta <q<\delta$ なる任意の $q\in$   $\mbox{${\mathbb{Q}}$}$ にたいして、

$$1-\delta < 2^{-\delta} < 2^q< 2^{\delta} < 1+ \delta$$

がなりたつ。すなわち、

$$\vert q\vert< \delta \implies \vert 2^q-1\vert<\epsilon$$

が言えることが分かった。