![]()
今回は、総復習の意味もこめて、レポート12 の解答を述べるとともに、 不定形の極限の扱いについて少し補足することにする。
レポート12 は、
![]() のときの問題であるが、
それを
のときの問題であるが、
それを ![]() の極限に作りかえたければ、変数を変換してたとえば
の極限に作りかえたければ、変数を変換してたとえば
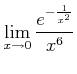
を求める問題を考えれば良い。
もっと一般に、
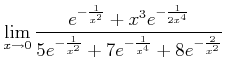
などの極限の計算も、どの項が大きくなるか目星がついておれば、 大変楽に計算できる。
(今回はレポートはありません。)
来週は試験です。
持ち込み:他の人の邪魔にならないもの、通信機能を持たないものならば、 何でも可。
試験にでそうな問題:
◯上の極限はいくらだろうか。(答え:
![]() .)
.)
◯
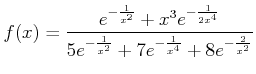
とおいたとき、
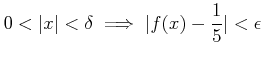
をみたすようにするには、
◎期限を過ぎたレポートは、特例欠席等の正当の理由がない限り 受け取りませんのであしからず御了承ください。。
問題12.1 解答。
解答にうつる前に、記号を説明しておこう。
実数 ![]() にたいして、
にたいして、![]() より大きい整数が存在する。
(アルキメデスの原理。)その一つを
より大きい整数が存在する。
(アルキメデスの原理。)その一つを ![]() としよう。
また、
としよう。
また、![]() 以下の整数が存在することも(
以下の整数が存在することも(![]() に対してアルキメデスの原理
を適用することにより)分かる。その一つを
に対してアルキメデスの原理
を適用することにより)分かる。その一つを ![]() としよう。
すると、
としよう。
すると、![]() 以下の整数のうち
以下の整数のうち ![]() 以上のものは
以上のものは
という有限個の整数のリストのなかに含まれており、とくに
と書く。言い換えれば、
| (☆) |
解答を始めよう。まず、
により、
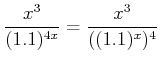 |
||
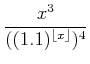 |
||
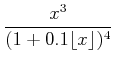 (二項定理) (二項定理) |
||
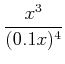 (← ☆) (← ☆) |
||
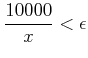 |
この範囲の ![]() に対してはもちろん
に対してはもちろん
![]() であるから、
であるから、
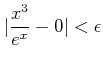
がなりたつことが分かった。
解説 いわゆる不定形の極限の問題である。
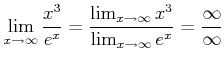
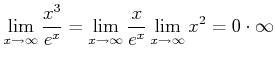
などとやっても、極限は求まらない。 「
では不定形の極限はどのように扱えば良いかと言えば、この問題で言えば ![]() と
と ![]() との大きくなりかたの競争を観察することになる。
講義でも少し述べたように、この競争はハッキリ「カタ」がついていて、
かなり控え目に見積もっても
との大きくなりかたの競争を観察することになる。
講義でも少し述べたように、この競争はハッキリ「カタ」がついていて、
かなり控え目に見積もっても ![]() が圧勝する。上記解答はそのような見積もりの
一方法である。
が圧勝する。上記解答はそのような見積もりの
一方法である。
二項定理を巾指数が整数でない場合にも用いている解答が多かったが、 厳密には本講義では巾指数が正の整数の場合しか扱っていない。 したがって上記解答のように少し工夫が必要である。