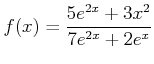
にたいして、 極限
を.考えたい。
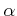 の値を求めなさい。(答のみでよい。)
の値を求めなさい。(答のみでよい。)
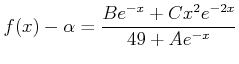
を満たす定数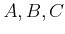 を求めなさい。
を求めなさい。
- 適当な正の数
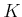 をとると、
をとると、
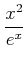 は
は 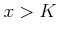 の範囲で有界であることを示しなさい。
(分かりにくい場合には、
「
の範囲で有界であることを示しなさい。
(分かりにくい場合には、
「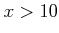 ならば
ならば
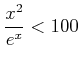 であることを示しなさい。」
という風に読みかえて解いても良い。)
であることを示しなさい。」
という風に読みかえて解いても良い。)
- 正の実数
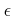 に対して、
に対して、
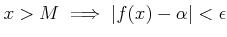
を満たす実数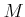 を一つ求めなさい。
(本小問では理由をきちんと書くことがが大事である。)
を一つ求めなさい。
(本小問では理由をきちんと書くことがが大事である。)
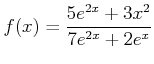
にたいして、 極限
を.考えたい。
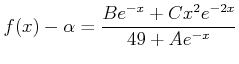
を満たす定数
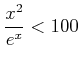 であることを示しなさい。」
という風に読みかえて解いても良い。)
であることを示しなさい。」
という風に読みかえて解いても良い。)
を満たす実数
試験解答:
(1)
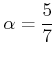 .
.
(2)
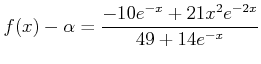
すなわち、
(3)
まず分母の見積もりをしよう。
実数 ![]() にたいして、その整数部分
にたいして、その整数部分
![]() のことを
のことを
![]() と書くと、
と書くと、![]() のとき
のとき
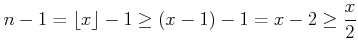
に注意すると、
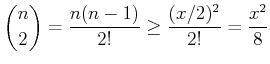 |
そこで、同じ範囲、すなわち ![]() で
で
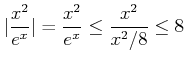 |
(4)
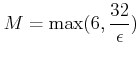
とおくとよい。実際、任意の
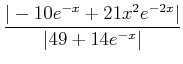 |
||
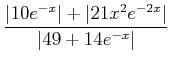 (三角不等式) (三角不等式) |
||
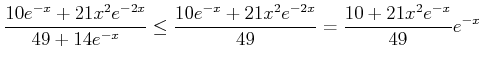 |
||
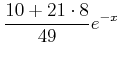 ((3)による) ((3)による) |
||
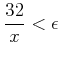 |