


Next: About this document ...
解析学 IA No.1要約
 《多変数関数》
《多変数関数》
本講義では多変数の関数の扱い方、とくに極限と微分について講述する。
教科書には二変数関数を中心に書かれているが、考え方は変数が増えても同じである。
定義 1.1
一般に, 正の整数
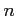
に対して、
を、(実)
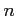
次元空間と呼ぶ。(2次元空間のことを平面、
3次元空間のことを単に空間と呼ぶ。)
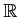
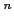
の元を(親しみをこめて)
点とよぶ。
高次元の空間について、非日常的だと思う人もいるかも知れないが、
そうではない。それらは変数の空間として大事な意味を持つ。
変数を多くもつ関数などというのはいくらでも出会うだろう。
一般に、
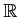
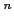 全体で関数が定義されていることは少なく、
全体で関数が定義されていることは少なく、
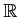
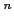 の部分集合
の部分集合 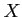 のみで定義される場合がほとんどである。
ところが極限、微分を論じる時には、考えている集合
のみで定義される場合がほとんどである。
ところが極限、微分を論じる時には、考えている集合 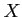 の
「ハジッコ」での話がややこしい場合がある。
そこで、ハジッコがない集合には特別な名前をつけて、それを
愛用するのである。
の
「ハジッコ」での話がややこしい場合がある。
そこで、ハジッコがない集合には特別な名前をつけて、それを
愛用するのである。
上の命題の証明には内積の概念を用いるのが便利である。
補題 1.1
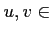
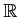
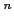 にたいして、
それらの内積を
にたいして、
それらの内積を
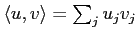 で定義する。
このとき、
で定義する。
このとき、
-
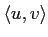 は
は 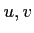 について双線型である。
について双線型である。
-
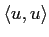 は非負の実数である。その平方根を
は非負の実数である。その平方根を 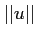 と書く。
と書く。
-
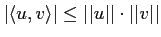 ,
,
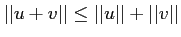 .
.
-
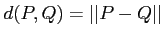 .
.
定義 1.3
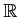
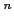
の部分集合
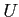
が
開集合であるとは
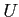
の任意の点
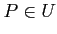
にたいして、 ある正の実数
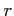
が存在して、
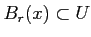
であるときにいう。一行で書くと:
またもや 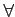 と
と 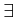 がでてきた。この講義でも大事になるので
使い方をマスターして頂きたい。とくに、
がでてきた。この講義でも大事になるので
使い方をマスターして頂きたい。とくに、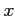 と
と 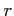 の登場の順番を気にして
欲しい。
の登場の順番を気にして
欲しい。
定義 1.4
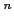
の点列
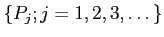
が点
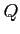
に
収束するとは、
のときにいう。
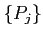
が
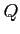
に収束するとき、
とか、
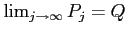
と書く。
つまり点列の極限を数(距離)の極限に帰着させているのである。
数の極限は 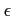 -
-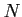 法を用いて定義されることを思い出しておくこと。
法を用いて定義されることを思い出しておくこと。
補題 1.2
点列の収束は、その各成分が収束することと同値である。
定義 1.5
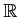
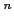
の部分集合
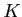
が
閉集合であるとは、「
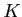
に属する点からなる
点列
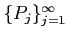
が
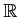
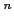
の点
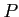
に収束するなら、
必ず
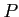
も
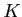
に属する」ときに言う。
定義 1.6
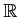
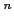
の部分集合
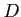
が
領域 であるとは、
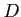
内の任意の二点
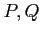
が
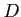
内の折れ線で結べるときに言う。
定義 1.7
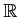
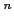
の部分集合
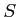
が
有界 であるとは、
ある
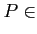
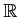
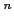
と
ある正の実数
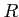
があって、
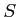
が
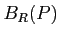
のなかにすっぽりと
部分集合として含まれてしまうときに言う。
補題 1.3
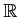
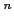 の部分集合
の部分集合 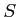 に対して、次の二条件は同値である。
に対して、次の二条件は同値である。
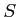 は閉集合である。
は閉集合である。
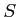 の
の
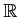
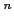 での補集合
での補集合
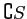 は開集合である。
は開集合である。
下の例のように、「開集合」「閉集合」は
「どの集合のなかで考えるか」が大切である
定義 1.8
写像(関数)
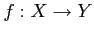
が与えられているとき、
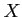
のことを
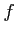
の
定義域(もしくは始集合),
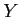
のことを
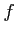
の
終集合
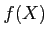
のことを
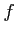
の
値域とよぶのであった。
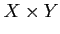
の
部分集合
のことを
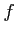
の
グラフとよぶ。
※レポート問題
(期限:次の講義の終了時まで。)
問題 1.1
平面
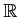
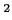
の部分集合
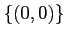
(一点からなる集合)は
開集合ではないことを示しなさい。



Next: About this document ...
2009-04-06
![]() 《多変数関数》
《多変数関数》
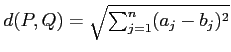 で定義する。
で定義する。
![]()
![]() 全体で関数が定義されていることは少なく、
全体で関数が定義されていることは少なく、
![]()
![]() の部分集合
の部分集合 ![]() のみで定義される場合がほとんどである。
ところが極限、微分を論じる時には、考えている集合
のみで定義される場合がほとんどである。
ところが極限、微分を論じる時には、考えている集合 ![]() の
「ハジッコ」での話がややこしい場合がある。
そこで、ハジッコがない集合には特別な名前をつけて、それを
愛用するのである。
の
「ハジッコ」での話がややこしい場合がある。
そこで、ハジッコがない集合には特別な名前をつけて、それを
愛用するのである。
![]() と
と ![]() がでてきた。この講義でも大事になるので
使い方をマスターして頂きたい。とくに、
がでてきた。この講義でも大事になるので
使い方をマスターして頂きたい。とくに、![]() と
と ![]() の登場の順番を気にして
欲しい。
の登場の順番を気にして
欲しい。