![]() 《偏微分と全微分》
《偏微分と全微分》
多変数関数から、「他の変数を止めて一つだけの変数に着目する」ことにより、 一変数関数を得ることができる。その意味で多変数関数はの微積分について、 ある程度は知っていることになる。
を考えたときに、これが
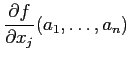 とか
とか 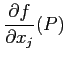 とか
とか などと書く。
偏微分係数は、「一つの変数だけを少しだけ動かすとどうなるか」について語ってくれる 数である。ではいろいろな変数をそれぞれ少しだけ動かすとどうなるだろうか?
と書いて、
多変数の微分はベクトルと行列の記法を使ったほうがすっきりする。
以下では
![]()
![]() や
や
![]()
![]() の元は
(紙面の都合で横に書いている場合もあるが、基本的には全部)
「縦ベクトル」だと思って頂きたい。
の元は
(紙面の都合で横に書いている場合もあるが、基本的には全部)
「縦ベクトル」だと思って頂きたい。
が成り立つときにいう。
全微分は、![]() の一次近似を与える。偏微分は
の一次近似を与える。偏微分は ![]() が軸方向から
が軸方向から ![]() に近づくときの
に近づくときの ![]() の挙動を与えているから、全微分が分かっていれば
偏微分は自動的に全微分から計算できることになる。
の挙動を与えているから、全微分が分かっていれば
偏微分は自動的に全微分から計算できることになる。
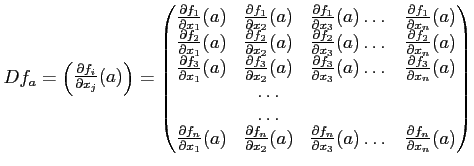
実用上は、偏微分のデータを用いて全微分の行列成分を得るという風に 上の定理が使われることが多い。
※レポート問題
(期限:次の講義の終了時まで。)