解析学 IA No.8要約

一次近似、二次近似。(まとめ)

$f$ の微分とは、$f$ の一次近似のことなのであった。 言い換えると、ベクトル $a$ と $h=(h_i)$ とに対して、

$$f(a+h)=f(a)+\sum_i f_{x_i}(a) h_i + o(\vert\vert h\vert\vert).$$

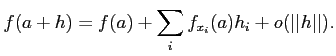
微分を一次近似の言葉で解釈することにより、様々な公式が理解しやすくなり、 覚えやすくなる。これは一変数でもそうで、例えば、

$$(f\circ g)'(a)=f'(g(a)) g'(a)$$

は

$$g(a+h)=g(a)+ g'(a) h +o(\vert h\vert)$$

と

$$f(u+v)=f(u)+f'(u) v + o(\vert v\vert)$$

という一次近似の合成として理解できる。

$f$ のテイラー展開とは、さらに高次の項も含めて近似を良くすることに相当する。 例えば、$f$ の二次近似は

$$f(a+h)=f(a)+\sum_i f_{x_i}(a) h_i +\frac{1}{2} \sum_{i,j} f_{x_i x_j} h_i h_j+ o(\vert\vert h\vert\vert^2).$$

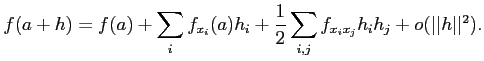
である。 とくに、二変数では、

$$f(a+h,b+k) =f(a,b)+f_{x}(a,b)h + f_y(a,b) k$$

$$+ \frac{1}{2} f_{xx}(a,b) h^2 +2 f_{xy}(a,b) hk +f_{yy}(a,b) k^2 +o(\vert\vert h,k\vert\vert^2)$$

という具合に書ける。 二次近似が特に目だった働きを見せるのは、$Df(a)=0$ すなわち、$f$ の $1$ 次 近似が消えてしまっているときである。そのときには二次の項がクローズアップされる ことになる。 二変数の場合でいえば、 $f_x(a,b)=0$ かつ $f_y(a,b)=0$ のとき、

$$f(a+h,b+k)=f(a,b) +\frac{1}{2} f_{xx}(a,b) h^2 +2 f_{xy}(a,b) hk +f_{yy}(a,b) k^2 +o(\vert\vert h,k\vert\vert^2)$$

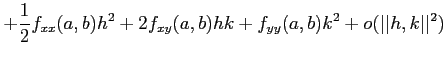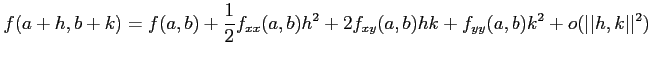
が成り立つことを意味している。これは、$f$ の $(a,b)$ の付近での挙動が 大まかに 二次式で記述できるということを言っている。

教科書の``定理4.11(極値の判定法)''はその考えに基づいており、 証明の考え方は一変数の場合に準ずる。

但し二次形式の扱い方という高次元の問題が残っていた。 これについては線形代数学で扱う(かも知れない。)

二変数二次形式は例外的にやさしい。これは本質的に一変数の二次式を 扱うのと同等に扱えるからである。たとえば

$$x^2+2xy+ y^2 =(x+y)^2, \quad x^2+2xy+ 2y^2 =(x+y)^2+y^2$$

はそれぞれ

$$x^2+2 x + 1= (x+1)^2 ,\quad x^2+2 x + 2= (x+1)^2+1$$

に対応している。(この考え方は式の斉次化、非斉次化の話として一般化される。)

※レポート問題 (期限：次の講義の終了時まで。)

問題 8.1   一変数のテイラー展開の知識を用いて、 固定した $t$ について

$$\sin(t+\Delta t)=\sin(t)+ c_1 \Delta t + c_2 (\Delta t)^2 +o(\vert\Delta t\vert^2)$$

をみたす $c_1$ , $c_2$ を求めなさい。(剰余項の評価等の詳細は問わない。) さらに、 $f(x,y)=x^2 y$ にたいして、 $f(a+h,b+k)$ を $h,k$ について整理したものを上記の式に代入することにより、 $\sin(x^2 y)$ の $a,b$ における 2次近似を求めなさい。