![]() 逆写像定理。
逆写像定理。
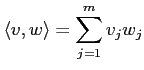
で定義する。
で定義する。
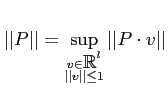
で定義する。
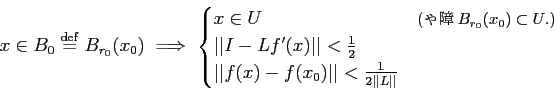
がなりたつ。
上の定理の証明のキモは、以下の補題(Newton 法)である。
ただし、![]() の逆行列のところを、
の逆行列のところを、
![]() で置き換える部分が、本物の Newton 法とは異なる。
で置き換える部分が、本物の Newton 法とは異なる。
すると、
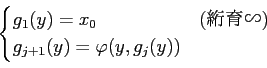
すると
のとき、
とくに、
逆写像定理では、定義域と値域の次元が等しく、
なおかつ点 ![]() での
での ![]() の微分
の微分
![]() が
可逆であることが適用のポイントである。
しかし、下のような考え方を用いて、
定義域と値域の次元が違う場合にも、逆関数の定理を応用することができる。
ここでは大まかな考え方のみ書いておこう。(詳細は乞御研究)
が
可逆であることが適用のポイントである。
しかし、下のような考え方を用いて、
定義域と値域の次元が違う場合にも、逆関数の定理を応用することができる。
ここでは大まかな考え方のみ書いておこう。(詳細は乞御研究)
が
が存在する。 すなわち、
をすべての
※レポート問題
(期限:次の講義の終了時まで。)
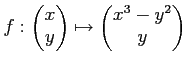
なる(二変数ベクトル値)関数の