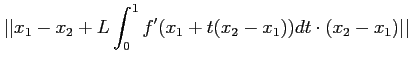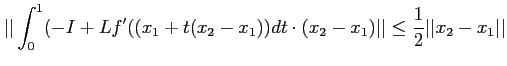Next: About this document ...
解析学 IA No.10要約
 多変数関数の(リーマン)積分
多変数関数の(リーマン)積分
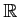
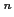 の部分集合
の部分集合
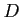 上で定義された実数値もしくはベクトル値関数
上で定義された実数値もしくはベクトル値関数 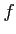 に対して、
に対して、
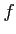 の
の 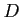 上の積分(定積分)は次のように定義される。
上の積分(定積分)は次のように定義される。
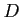 を小さい部分集合
を小さい部分集合 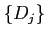 の和に分ける。
の和に分ける。
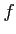 を 各
を 各 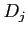 上で定数値関数
上で定数値関数 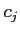 で近似する。
で近似する。
- 積分値の一つの近似として、
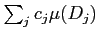 を得る。
ただし
を得る。
ただし 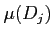 は
は 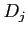 の体積である。
の体積である。
- 細分
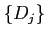 を細かくしたとき、上のような近似が近づく値があるなら、
それを
を細かくしたとき、上のような近似が近づく値があるなら、
それを 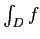 と定義する。
と定義する。
問題がいくつかある。
- 小さい集合
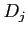 の体積
の体積 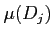 は如何に定義されるだろうか。
これには次元
は如何に定義されるだろうか。
これには次元 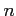 について帰納的に議論し、
について帰納的に議論し、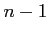 次元の積分で定義するか、
もしくは
次元の積分で定義するか、
もしくは 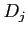 として直方体のような限定的なもののみを扱う方法がある。
として直方体のような限定的なもののみを扱う方法がある。
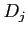 として直方体のような限定的なものを使う場合、
として直方体のような限定的なものを使う場合、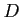 をそのようなもので
過不足なく覆うことが難しくなる。
これには若干の「はみ出し」もしくは「不足部分」を許して、
あとでそれらの寄与が十分小さくなることを示す方法がある。
をそのようなもので
過不足なく覆うことが難しくなる。
これには若干の「はみ出し」もしくは「不足部分」を許して、
あとでそれらの寄与が十分小さくなることを示す方法がある。
- 細分を細かくするとき、はたして本当に和
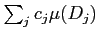 は
小さくなるだろうか。これは
は
小さくなるだろうか。これは 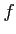 がどのような関数かによって変わってくる。
(コンパクト集合上の連続関数なら各
がどのような関数かによって変わってくる。
(コンパクト集合上の連続関数なら各 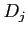 上で一様近似できるだろう。)
上で一様近似できるだろう。)
- このような積分は座標の取り方によらないだろうか? (「直方体」は
明白に座標の取り方に依存する。すなわち、直方体は座標変換すると別のモノになって
しまう。)
リーマン積分はこれらの問題点に解答を与えるが、十分とは言えない。
徹底的に解決するためにはルベーグ積分をオススメする。
そうは言っても、「なんでもかんでもルベーグ積分」では成金趣味が見えかくれして
イヤなので、ちょっとぐらいは扱っておこう。
命題 10.1
ジョルダンの外測度の定義で、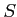 を覆う区間直方体は互いに交わらない
もののみに限定しても結果はおなじである。
を覆う区間直方体は互いに交わらない
もののみに限定しても結果はおなじである。
上の命題はジョルダン流の、「有限の区間直方体で覆う」から正しい
命題で、ルベーグ流の、「可算個で覆う」方法ではもはやなりたたない。
系 10.2
- 区間直方体は測度確定であり、
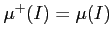 .
.
- 一般の有界集合
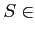
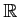
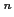 にたいして、
にたいして、
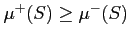 がなりたつ。
がなりたつ。
上のことがあるから、
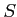 測度確定の場合に
測度確定の場合に 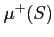 のことを単に
のことを単に 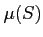 と書いても差し支えない。
と書いても差し支えない。
問題 10.1
平面三角形
を区間長方形で覆って、
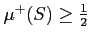
を証明しなさい。
逆写像定理の証明
定理9.1 の記号でつぎのような計算を行うと、
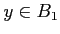 を止めるごとに、
を止めるごとに、
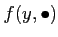 が縮小写像であること
(したがって補題9.3が正しいこと)が言える。
が縮小写像であること
(したがって補題9.3が正しいこと)が言える。
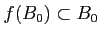 も証明すべきだが、それは「練習問題」として
残しておこう。(レポート問題ではない。))
も証明すべきだが、それは「練習問題」として
残しておこう。(レポート問題ではない。))
上の補題の主張(3)により、補題9.3 の「各点収束」は実は「一様収束」と
言っても正しいことが分かる。連続関数の一様極限は連続であるから、
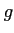 は連続関数である。
は連続関数である。
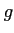 の定義により、
の定義により、
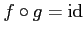 であることは容易に分かる。あとは
研究に任せよう。
であることは容易に分かる。あとは
研究に任せよう。



Next: About this document ...
2009-06-26
![]() 多変数関数の(リーマン)積分
多変数関数の(リーマン)積分
![]()
![]() の部分集合
の部分集合
![]() 上で定義された実数値もしくはベクトル値関数
上で定義された実数値もしくはベクトル値関数 ![]() に対して、
に対して、
![]() の
の ![]() 上の積分(定積分)は次のように定義される。
上の積分(定積分)は次のように定義される。
![]() 測度確定の場合に
測度確定の場合に ![]() のことを単に
のことを単に ![]() と書いても差し支えない。
と書いても差し支えない。
![]() を止めるごとに、
を止めるごとに、
![]() が縮小写像であること
(したがって補題9.3が正しいこと)が言える。
が縮小写像であること
(したがって補題9.3が正しいこと)が言える。
![]() も証明すべきだが、それは「練習問題」として
残しておこう。(レポート問題ではない。))
も証明すべきだが、それは「練習問題」として
残しておこう。(レポート問題ではない。))