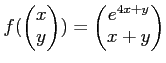
により定義する。このとき、
- 偏微分
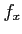 ,
, 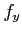 をそれぞれ求めなさい。
をそれぞれ求めなさい。
- 点
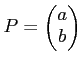 における
における 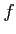 の
全微分
の
全微分
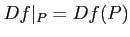 (どちらの書き方で書いても同じモノを意味する)、
および その行列式
(どちらの書き方で書いても同じモノを意味する)、
および その行列式
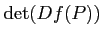 を求めなさい。
を求めなさい。
- 点
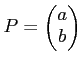 における
における 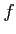 の二次近似を
求めなさい。
の二次近似を
求めなさい。
![$\displaystyle D=[0,1] \times [0,1]
$](img12.png)
とし、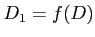 とおく。このとき、
とおく。このとき、
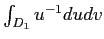 を
を
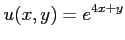
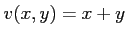
と変数変換をすることにより求めなさい。( により
により 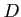 の点と
の点と  の点とが
全単射で対応することは証明なしに自由に使ってよいことにする。)
の点とが
全単射で対応することは証明なしに自由に使ってよいことにする。)
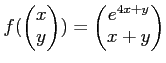
により定義する。このとき、
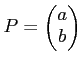 における
における 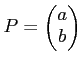 における
における
とし、
ちなみに ![]() は次のような領域である。
は次のような領域である。
![\includegraphics[scale=0.5]{mondai.eps}](img19.png)
![\includegraphics[scale=0.5]{mondai1.eps}](img20.png)
結果については理学部二号棟6F 数学掲示板で行なう。採点等の処理は3日から一週間程度 かかる予定。掲示までは 成績についての質問には一切応じられない。
解答
(1)
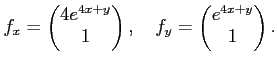
(2)
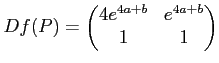
したがって、その行列式は
である。
(3)
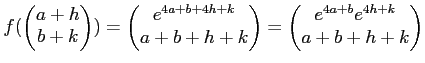 |
||
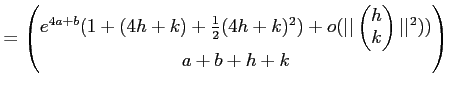 |
||
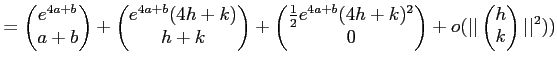 |
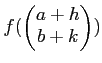 |
||
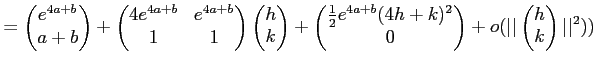 |
||
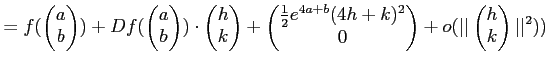 |
なお、上の解答を見れば想像がつくように、(1) は(2)の ![]() の列ベクトルを見れば
よい(逆に言えば、(2)の前半は(1)の答えを単に並べれば良い)し、
(3)の一次の項を取り出せば、(1)および(2)の前半が自動的に得られる。
の列ベクトルを見れば
よい(逆に言えば、(2)の前半は(1)の答えを単に並べれば良い)し、
(3)の一次の項を取り出せば、(1)および(2)の前半が自動的に得られる。
(4)
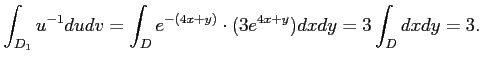
変数変換で気をつけなければならないのは、