


Next: Bibliography
Cohomologies.
Yoshifumi Tsuchimoto

Let
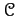 be an abelian category. For any object
be an abelian category. For any object 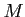 of
of
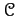 ,
the extension group
,
the extension group
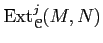 is defined to be the derived functor of
the ``hom'' functor
is defined to be the derived functor of
the ``hom'' functor
We note that the
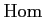 functor is a ``bifunctor''.
We may thus consider the right derived functor of
functor is a ``bifunctor''.
We may thus consider the right derived functor of
 and that of
and that of
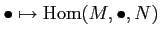 .
Fortunately, both coincide:
The extension group
.
Fortunately, both coincide:
The extension group
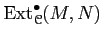 may be calculated by using either an
injective resolution of the second variable
may be calculated by using either an
injective resolution of the second variable 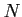 or
a projective resoltuion of the first variable
or
a projective resoltuion of the first variable 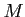 .
See [1, Proposition 8.4,Corollary 8.5].
.
See [1, Proposition 8.4,Corollary 8.5].
EXAMPLE 06.1
Let us compute the extension groups
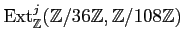
.
- We may compute them by using an injective resolution
of
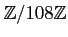 .
.
- We may compute them by using a free resolution
of
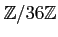 .
.
EXERCISE 06.1
Compute an extension group
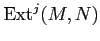
for modules
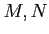
of your choice.
(Please choose a non-trivial example).
In the last lecture we mentioned the notion of injective hulls.
Although they are not essential part of our lecture,
students may find it interesting to calculate some of the injective hulls
of known modules.
So we write down some definitions and results related to them.
DEFINITION 06.2
Let
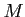
be an
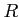
-module. An
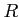
-module
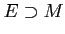
is called an
essential extension of
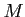
if every non-zero submodule of
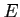
intersect
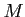
non-trivially. We denote this as
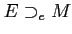
.
Such an essential extension is called maximal if no module properly containing E is an essential extension of M .
LEMMA 06.3
A module 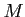 is injective if and only if
is injective if and only if 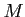 has no proper essential extensions.
has no proper essential extensions.
THEOREM 06.5
For any 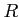 -module
-module 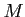 , there exists an injective module
, there exists an injective module 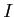 which contains
which contains
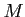 whichis minimal among such. The module
whichis minimal among such. The module 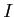 is unique up to a (non-unique)
isomorphism.
is unique up to a (non-unique)
isomorphism.
DEFINITION 06.6
Such
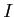
in the above theorem is called the
injective hull of
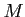
.
Injective
hulls may then be used to obtain the ``minimal injective resolution''
of a module.
EXAMPLE 06.7
Let
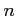
be a positive integer.
The injective hull of a
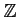
-module
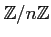
is equal to
![$ \mathbb{Z}[\frac{1}{n}]/n\mathbb{Z}$](img29.png)
.
Thus an injective resolution of
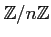
is given as follows.



Next: Bibliography
2010-06-03
![]() be an abelian category. For any object
be an abelian category. For any object ![]() of
of
![]() ,
the extension group
,
the extension group
![]() is defined to be the derived functor of
the ``hom'' functor
is defined to be the derived functor of
the ``hom'' functor
![]() functor is a ``bifunctor''.
We may thus consider the right derived functor of
functor is a ``bifunctor''.
We may thus consider the right derived functor of
![]() and that of
and that of
![]() .
Fortunately, both coincide:
The extension group
.
Fortunately, both coincide:
The extension group
![]() may be calculated by using either an
injective resolution of the second variable
may be calculated by using either an
injective resolution of the second variable ![]() or
a projective resoltuion of the first variable
or
a projective resoltuion of the first variable ![]() .
See [1, Proposition 8.4,Corollary 8.5].
.
See [1, Proposition 8.4,Corollary 8.5].
![$\displaystyle 0\to \mathbb{Z}/n\mathbb{Z}\to \mathbb{Z}[\frac{1}{n}]/n \mathbb{Z}\to \mathbb{Z}[\frac{1}{n}]/\mathbb{Z}\to 0
$](img30.png)