第5回目の主題 :
![]()
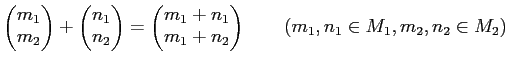
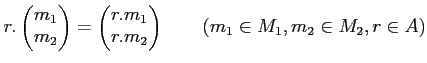
この加群を
有限個の ![]() -加群
-加群
![]() の直和
の直和
![]() も
同様に定義される。
同じ加群
も
同様に定義される。
同じ加群 ![]() の
の ![]() 個の直和
個の直和
![]() のことを
のことを
![]() と書く。
と書く。
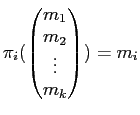
で定義される
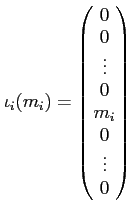 ($i$ 番目の成分のみ $m_i$ であとは $0$.)
($i$ 番目の成分のみ $m_i$ であとは $0$.)
で定義される
直和の間の写像は次のように行列的に分解できる。
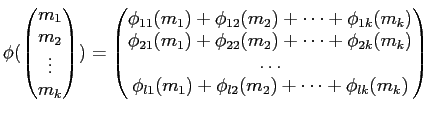
と分解される。ここに
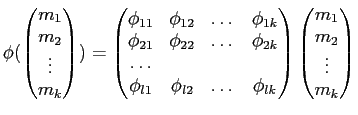
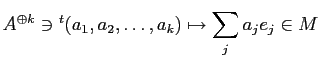
は同型である1。 とくに、
は
が成り立つ。
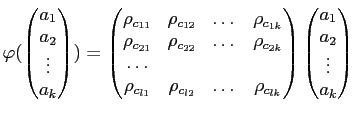
と書ける。
と書き表す。
(下記の問題のように) ![]() に
に ![]() -加群以外の構造がある場合には、
区別のため上の意味の
-加群以外の構造がある場合には、
区別のため上の意味の
![]() のことを
のことを
![]() 等と書くことがある。
等と書くことがある。
を示しなさい。