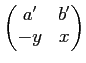Next: About this document ...
代数学II要約 No.7
第7回目の主題 :

定義 7.1
環
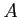
上の加群
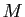
の元
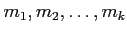
に対して、
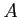
-準同型
の核
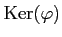
の元のことを
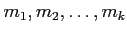
の
関係式と呼び、
その全体のなす加群
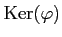
のことを
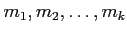
の
関係式のなす加群と呼ぶ。
以下では、次のような変換を考える。
- 変換1.
-
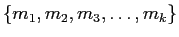 の順序を入れ換える。
の順序を入れ換える。
- 変換2.
-
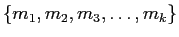 の代わりに
それを
の代わりに
それを
 で「ひねった」
で「ひねった」
を考える。
- 変換3.
-
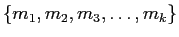 の代わりに
の代わりに 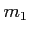 を
を
に置き換えたもの
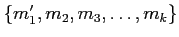 を考える。
を考える。
(変換3)は(変換1), (変換2)を有限回組み合わせて得られることが
わかるので
以下の議論で必須ではない。
補題 7.2 (変換1)
,(変換2),(変換3)の形の変換は(同じ形の)逆変換をもつ。
とくに、
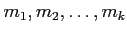
が
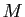
を生成するならば、それに
(変換1),(変換2),(変換3) を有限回繰り返して得られた組み合わせ
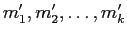
も
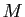
を生成する。
上の補題のような 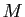 と
と
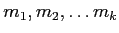 が与えられたとき、
が与えられたとき、
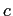 に当たるものの候補を見付け、
もしそれが「本物」ではない場合には証明にあるような操作を用いて
生成元の変換を逐次行うことにより、
に当たるものの候補を見付け、
もしそれが「本物」ではない場合には証明にあるような操作を用いて
生成元の変換を逐次行うことにより、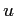 を求めるアルゴリズムを
作成することができる。同様にして次の定理の
を求めるアルゴリズムを
作成することができる。同様にして次の定理の 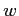 を得るアルゴリズムも
得られる。
を得るアルゴリズムも
得られる。
定理 7.4
可換 PID
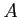
上の有限生成加群
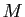
が与えられているとする。
このとき、
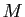
の生成系
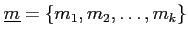
にたいして、
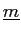
を(変換1),(変換2),(変換3)を有限回繰り返すことにより、
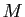
の新しい生成系
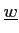
であって、
となるものが存在する。
定義 7.5
一つの元で生成される加群を巡回加群と呼ぶ。
命題 7.7 (定理の言い換え)
可換 PID
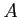
上の任意の有限生成加群
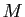
は巡回
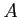
加群の直和に同型である。
ゆえに、ある
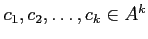
と
なる同型が存在する。
(ただの)加群は
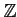 -加群のことと同じであって、
-加群のことと同じであって、
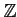 は
は 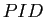 であることから、
つぎの(大変有用かつ重要な)系が成り立つ。
であることから、
つぎの(大変有用かつ重要な)系が成り立つ。
系 7.8 (有限生成アーベル群の基本定理)
任意の有限生成アーベル群は巡回群の有限個の直和である。
問題 7.1
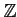
-加群
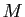
が2つの元
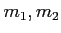
で生成されていて、次の関係式を満たすとする。
これ以外に特段の関係式がないとするとき、
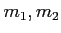
に(変換1),(変換2),(変換3)
を有限回施すことにより、新しい生成元
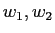
を得て、
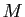
を巡回加群の直和として表現せよ。
復習:
命題 7.9
可換 PID
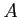
の元
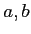
に対して、イデアル
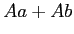
は
ある単項イデアル
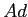
と等しい。このとき、ある
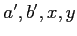
が存在して、
次の二式が成り立つ。
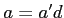 ,
, 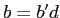 .
.
-
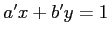 .
.
とくに、
は
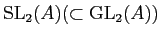
の元である。
命題 7.10
可換 PID
のイデアルの増加列
は必ず有限で止まる。すなわち、ある
があって、
が成り立つ。



Next: About this document ...
2010-06-01
![]()
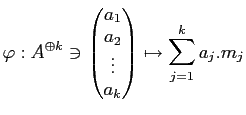
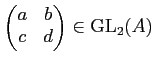 で「ひねった」
で「ひねった」
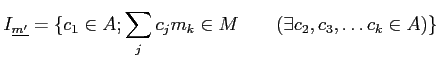
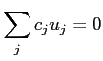
![]() と
と
![]() が与えられたとき、
が与えられたとき、
![]() に当たるものの候補を見付け、
もしそれが「本物」ではない場合には証明にあるような操作を用いて
生成元の変換を逐次行うことにより、
に当たるものの候補を見付け、
もしそれが「本物」ではない場合には証明にあるような操作を用いて
生成元の変換を逐次行うことにより、![]() を求めるアルゴリズムを
作成することができる。同様にして次の定理の
を求めるアルゴリズムを
作成することができる。同様にして次の定理の ![]() を得るアルゴリズムも
得られる。
を得るアルゴリズムも
得られる。
![]() -加群のことと同じであって、
-加群のことと同じであって、
![]() は
は ![]() であることから、
つぎの(大変有用かつ重要な)系が成り立つ。
であることから、
つぎの(大変有用かつ重要な)系が成り立つ。