第8回目の主題 :
![]()
可換環 ![]() 上の加群
上の加群 ![]() の元
の元
![]() にたいして、
次のような変換を考えていた。
にたいして、
次のような変換を考えていた。
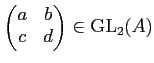 で「ひねった」
で「ひねった」
を考える。
に置き換えたもの
なる関係式をひとつ見つけてくる。このような関係式で非自明なものが 存在しないならば
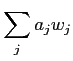
のうち、
なる関係式を見つけることができる。
上の手順で ![]() を定理7.4 にあるように直和分解できるが、
その際の
を定理7.4 にあるように直和分解できるが、
その際の ![]() は、補題7.3の (2)で言われるような極大性の条件を満足するとは
限らない。その要求を満たすには次の補題のようなステップが必要になる。
応用上は定理7.4の形で十分なことが多いので詳細は略す。
は、補題7.3の (2)で言われるような極大性の条件を満足するとは
限らない。その要求を満たすには次の補題のようなステップが必要になる。
応用上は定理7.4の形で十分なことが多いので詳細は略す。
で与えられているとき、(言い換えると、
のように変換(変換2)を施すと、
であたえられる。