第10回目の主題 :
![]()
生成元と関係式についての扱いについてもう少し補足しておこう。
環 ![]() が与えられているとする。
が与えられているとする。
![]() -加群
-加群 ![]() が
が
![]() で生成されていて、それらが
関係式
で生成されていて、それらが
関係式
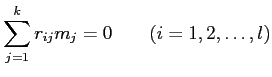 |
(関係R) |
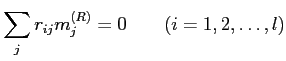 |
(関係 |
((関係 R) の ![]() を
を ![]() に変えたもの)をみたす。
に変えたもの)をみたす。
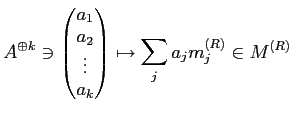
の核は
![]() -加群
-加群 ![]() が
が ![]() 個の元
個の元
![]() で生成されて、それらは関係式 (R)
をみたしたとする。
で生成されて、それらは関係式 (R)
をみたしたとする。
![]() を上記のように構成したとき、
を上記のように構成したとき、
![]() -加群の準同型
-加群の準同型
で
普遍性は代数の問題を考える上でキーになることが多い。
例えば、上の命題ような普遍性を持つ
![]() は
(適当な意味の)同型を除いて一意であることが証明できる。
は
(適当な意味の)同型を除いて一意であることが証明できる。
| (Rexample) |
として、
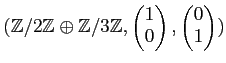 と同型である。)
と同型である。)
PID 上の有限生成加群 ![]() の構造は命題7.7のようによくわかっていて、
とくに
の構造は命題7.7のようによくわかっていて、
とくに ![]() は必ず有限表示であった。
は必ず有限表示であった。![]() の部分加群
の部分加群 ![]() が与えられたとき、
剰余加群
が与えられたとき、
剰余加群 ![]() に対して命題7.7 を用いることにより、次のことがわかる。
に対して命題7.7 を用いることにより、次のことがわかる。
上の命題は、 ネーター環上の任意の有限生成加群の任意の部分加群はまた有限生成である、 という性質の特別の場合である。
可換 PID 上の 有限生成加群の構造は、「単因子論」として知られる
ものと表裏一体の関係にある。これは次の理由による:
命題 10.2 によると、
一般に、環 ![]() の元を成分に持つ行列
の元を成分に持つ行列
が与えられれば構成 10.1 で有限表示
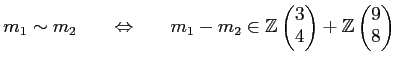
で定義し、
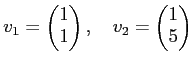
とおくと、