


Next: About this document ...
代数学II試験予想問題
- 持ち込みは他人の迷惑になるもの以外何でも可である。
- この予想問題と全く同じ問題は出ない。
- 知識のみの解答はほとんど0点に近いことを覚悟すること。
例えば下の問題15.1 の解答として「8と6とが互いに素ではないから」と書いても
(その事自体は正しいが、)ほとんど点にはならない。
問題 15.1
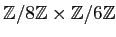
と
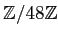
とは加群として同型ではないことを示しなさい。
問題 15.2
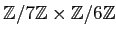
と
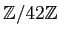
とは加群として同型であることを示しなさい。
問題 15.3
![$ {\mathbb{C}}[X]$](img5.png) -加群として
-加群として
![$ {\mathbb{C}}[X]/(X^2-1) \cong {\mathbb{C}}[X]/(X-1)\oplus {\mathbb{C}}[X]/(X+1)$](img6.png) であることを示しなさい。
であることを示しなさい。
2010-07-30
![]() -加群として
-加群として
![]() であることを示しなさい。
であることを示しなさい。 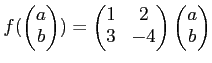
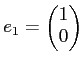 と
と
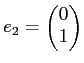 とは
とは