今日のテーマ:
![]()
ガロア理論とは、体の拡大をガロア群という群の構造を調べることにより 明らかにする理論である。 これにより代数方程式が手に取るように扱えるようになる。
ガロア理論はそれ自身代数幾何学や数論の重要な道具になったのみならず、 数学的対象をそれについての対称性により考察するという一般的原理の もととなって数学の爆発的発展の基礎を与えた。
例えば、
![]() 上の代数方程式
上の代数方程式
を考えよう。 この方程式の解を
のような数が必要になる。そして、これらの数同士の加減乗算による結果は 関係式(1.1)を用いればまたもや同様の数になる。
このような操作は、実は剰余環を用いることにより上手に扱える。
もっと一般に、体 ![]() 上の一変数多項式
上の一変数多項式 ![]() に対して、剰余環
に対して、剰余環
を考えると、この環における
つぎに、そのようにして作ったいろいろな環の 比較を行う必要がある。
例えば二次方程式
の解は
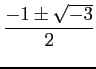
で与えられる。これは
と
の間に関係があることを意味している。