


Next: About this document ...
代数学III要約 No.3
今日のテーマ:

定義 3.1
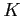
の 拡大体
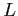
は
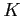
上のベクトル空間の構造を持つ。
そこで、
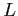
の
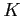
-ベクトル空間としての次元のことを
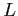
の
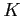
上の
拡大次数 といい、
![$ [L:K]$](img4.png)
で書き表す。
![$ [L:K]<\infty$](img5.png)
のとき、
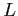
は
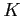
の
有限次拡大であると言う。
次の命題は体の拡大次数の方程式論的な意味を明らかにする。
定理 3.4
体
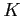
と、その拡大体
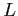
が与えられているとする。
このとき、
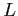
の 元で、
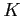
上代数的な元同士の和、差、積、商はまた
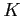
上代数的である。つまり、
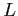
の元で
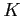
上代数的なものの全体
は体をなす。
補遺: 次のことは前回に述べるべきだったが、書いて置かなかったので
ここに改めて書いておくことにする。
(命題2.5の後あたりに配するのが妥当だったろう。)
問題 3.1
![% latex2html id marker 958
$ \alpha=\sqrt{2}+7\sqrt[3]{5}$](img19.png)
は
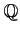
上代数的であることを示しなさい。
上の問題は間接的な解答でも良いわけだが、直接的に答える、
すなわち 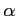 の
の
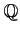 上の最小多項式を実際に求めることもできる。例えば次のようにすれば良い。
上の最小多項式を実際に求めることもできる。例えば次のようにすれば良い。
2010-10-15
![]()