


Next: About this document ...
代数学III要約 No.4
今日のテーマ:

共役は昔は共軛と書いた。したがって、
この字は「きょうやく」と読むのが正しい。
このへんの事情については wikipedia の共役の項にも記述が見られる。
ネットも捨てたもんじゃない。
体 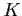 上の代数的数
上の代数的数 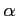 を付け加えてできた体
を付け加えてできた体 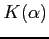 の構造は、
実際には
の構造は、
実際には 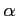 の
の 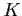 上の最小多項式
上の最小多項式 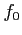 によって完全に決まるのであった。
によって完全に決まるのであった。
定義 4.1
体
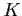
の拡大体
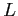
から
体
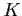
の拡大体
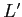
への写像
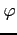
が
中への 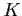 -同型
-同型であるとは、
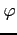
が環準同型であって、
なおかつ
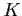
上で恒等写像に等しい時に言う。
言い換えると、
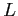
から
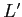
の中への
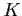
-同型とは環の準同型であって、
同時に
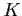
-線形写像でも
あるもののことである。
さらに、中への
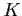
-同型
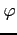
が全射であるとき、
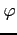
を単に
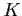 -同型
-同型と呼ぶ(このとき
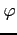
は必然的に全単射である) 。
定義 4.3
上の同値な条件のひとつ(ゆえに、全部)が成り立つとき、
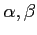
は
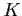
上
共役であるという。
問題 4.1
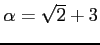
と
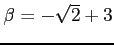
は
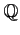
上共役ではあるが、
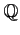
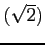
上共役ではないことを示しなさい。
(本問では
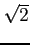
が無理数であることは証明なしに用いて良いことにする。)
問題 4.2
体
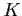
の拡大体
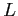
と、
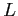
の元
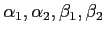
が
与えられているとする。
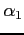
と
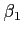
とが
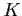
上共役で、
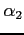
と
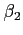
とが
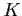
上共役ならば、
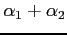
と
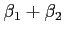
は
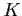
上共役であると
必ず言えるだろうか?
2010-10-22
![]()
![]() 上の代数的数
上の代数的数 ![]() を付け加えてできた体
を付け加えてできた体 ![]() の構造は、
実際には
の構造は、
実際には ![]() の
の ![]() 上の最小多項式
上の最小多項式 ![]() によって完全に決まるのであった。
によって完全に決まるのであった。