Next: About this document ...
代数学III要約 No.14
代数関数体
No.12 で (2),3,4次方程式の解法について述べた。
これは
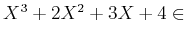
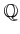
![$ [X]$](img3.png) のような具体的な多項式の
根を求めると見ることもできるが、別の見方もできる。すなわち、
(2次方程式の場合で言えば)多項式
のような具体的な多項式の
根を求めると見ることもできるが、別の見方もできる。すなわち、
(2次方程式の場合で言えば)多項式
の係数 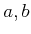 を不定元(変数)
とみて、そのような「普遍的な」2次多項式の根として
を不定元(変数)
とみて、そのような「普遍的な」2次多項式の根として
を考え、その特殊な場合として一般の2次の多項式を扱うという具合である。
定義 14.1
体
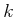
上の
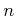
-変数多項式環
![$ k[X_1,X_2,\dots, X_n]$](img9.png)
の商体(多項式の
分数の形で書けるもの全体のなす体)を
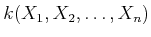
と書き、
体
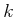
上の
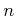 -変数有理関数体
-変数有理関数体と呼ぶ。
定義 14.2
体
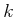
上の
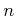
-変数有理関数体 の有限次代数拡大を
代数関数体と呼ぶ。
例 14.3
体
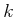
上の不定元
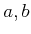
をとって2変数有理関数体
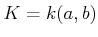
を考える。
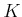
上の多項式
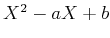
は
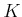
上既約であって、
その根の一つを
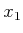
とおくと、
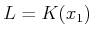
は2変数代数関数体の例である。
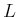
は
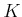
のガロア拡大で、
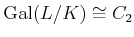
(2次の巡回群).
例 14.4
体
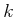
上の不定元
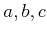
をとって3変数有理関数体
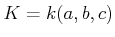
を考える。
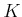
上の多項式
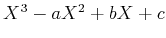
は
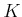
上既約であって、
その根を
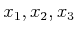
とおくと、
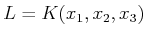
は2変数代数関数体の例である。
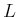
は
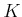
のガロア拡大で、
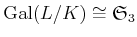
(3個の元の対称群).
上の例は一般の次数の「普遍多項式」の場合にまで拡張できる。
ガロア拡大で、そのガロア群が巡回群であるものを巡回拡大と呼ぶ。
上の命題は、「普遍的な」3次方程式の分解体が巡回拡大の繰り返しで
得られることを述べている。4次方程式についても同様のことができる。
有理関数体が出てきたついでに、次のことについても言及しておこう。
命題 14.6 (非分離拡大の例)
標数
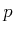
の体
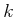
が与えられたとする。(例えば、
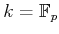
.)
このとき、
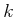
上の不定元
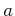
をひとつとって
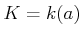
を考える。
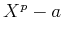
は
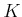
上既約であって、その根
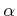
は
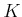
上分離的ではない。
問題 14.1
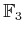
上の多項式
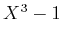
を因数分解せよ。
問題 14.2
上の命題
14.5 と同様の議論を4次方程式について
展開せよ。(少なくとも、
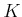
と
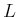
にあたるのものの中間体の
一つを見いだせ。)



Next: About this document ...
2011-01-24
![]()
![]()
![]() のような具体的な多項式の
根を求めると見ることもできるが、別の見方もできる。すなわち、
(2次方程式の場合で言えば)多項式
のような具体的な多項式の
根を求めると見ることもできるが、別の見方もできる。すなわち、
(2次方程式の場合で言えば)多項式