


Next: Bibliography
Commutative algebra
Yoshifumi Tsuchimoto
DEFINITION 01.1
A (unital associative)
ring is a set

equipped with two binary operations
(addition (``+'') and multiplication (``
'')) such that
the following axioms are satisfied.
- Ring-1.
 is an additive group with respect to the addition.
is an additive group with respect to the addition.
- Ring-2.
- distributive law holds. Namely, we have
- Ring-3.
- The multiplcation is associative.
- Ring-4.
 has a multiplicative unit.
has a multiplicative unit.
In this lectuer we are mainly interested in commutative rings,
that means, rings on which the multiplication satisfies the commutativity law.
For any ring  , we denote by
, we denote by 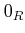 (respectively,
(respectively, 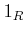 )
the zero element of
)
the zero element of  (respectively, the unit element of
(respectively, the unit element of  ).
Namely,
).
Namely, 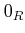 and
and 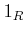 are elements of
are elements of  characterized by
the following rules.
characterized by
the following rules.
When no confusion arises, we omit the subscript `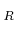 '
and write
'
and write 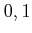 instead of
instead of 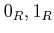 .
.
DEFINITION 01.2
A map
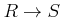
from a unital associative ring

to another unital associative ring
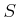
is said to be
ring homomorphism if it satisfies the following conditions.
- Ringhom-1.
-
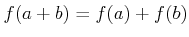
- Ringhom-2.
-
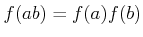
- Ringhom-3.
-
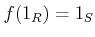
DEFINITION 01.5
Let
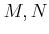
be modules over a ring

.
Then a map
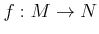
is called an
 -module homomorphism
-module homomorphism if
it is additive and preserves the

-action.
The set of all module homomorphisms from 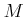 to
to 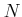 is denoted by
is denoted by
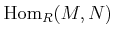 . It has an structure of an module in an obvious manner.
Furthermore, when
. It has an structure of an module in an obvious manner.
Furthermore, when  is a commutative ring, then it has a structure of
an
is a commutative ring, then it has a structure of
an  -module.
-module.
DEFINITION 01.6
An subset
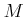
of an

-module
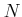
is said to be an
 -submodule
-submodule of
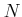
if
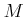
itself is an

-module and the inclusion map
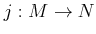
is an

-module homomorphism.
DEFINITION 01.7
An subset
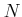
of an

-module
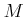
is said to be an
 -submodule
-submodule of
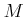
if
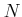
itself is an

-module and the inclusion map
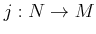
is an

-module homomorphism.
DEFINITION 01.8
Let

be a ring. Let
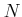
be an

-submodule of an

-module
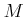
.
Then we may define the
quotient 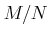
by
where the equivalence relation
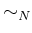
is defined as follows:
It may be shown that the quotient
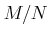
so defined is actually an

-module
and that the natural projection
is an

-module homomorphism.
DEFINITION 01.9
Let
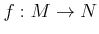
be an

-module homomorphism between

-modules.
Then we define its
kernel as follows.
The kernel and the image of an  -module homomorphism
-module homomorphism 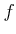 are
are  -modules.
-modules.
THEOREM 01.10
Let 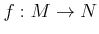 be an
be an  -module homomorphism between
-module homomorphism between  -modules.
Then
-modules.
Then
DEFINITION 01.11
Let

be a ring.
An ``sequence''
is said to be
an exact sequence of  -modules
-modules
if the following conditions are satisfied
- Exact1.
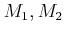 are
are  -modules.
-modules.
- Exact2.
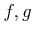 are
are  -module homomorphisms.
-module homomorphisms.
- Exact3.
-
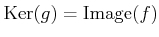 .
.
For any  -submodule
-submodule 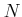 of an
of an  -module
-module 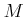 , we have the
following exact sequence.
, we have the
following exact sequence.
EXERCISE 01.1
Compute the following modules.
-
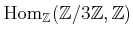 .
.
-
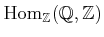 .
.
-
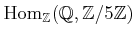 .
.
DEFINITION 01.12
Let
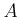
be an associative unital (but not necessarily commutative) ring.
Let
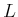
be a right
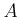
-module. Let
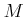
be a left
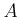
-module.
For any (
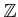
-)module
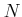
, an map
is called an
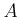 -balanced biadditive map
-balanced biadditive map if
-
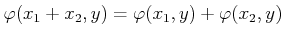
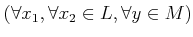 .
.
-
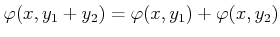
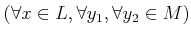 .
.
-
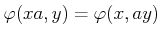
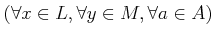 .
.
DEFINITION 01.14
We employ the assumption of the proposition above.
By a standard argument on universal objects, we see that such object is
unique up to a unique isomorphism. We call it
the
tensor product of
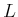
and
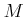
and denote it by
EXERCISE 01.2
Compute
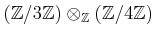
and
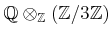
.
DEFINITION 01.16
A left
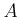
-module
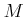
is said to be
flat if
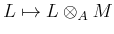
is an exact functor.
Namely, for any exact sequence
of left
-modules, the sequence
is also exact.
**The following two facts may give some intuitive idea of what flatness means.
THEOREM 01.17
If  is a Noetherian ring and
is a Noetherian ring and 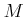 is a finitely-generated
is a finitely-generated  -module,
then
-module,
then 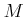 is flat over
is flat over 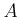 if and only if the associated sheaf
if and only if the associated sheaf 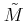 on
on
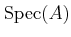 is locally free.
is locally free.
THEOREM 01.18
[1, Theorem 23.1+Theorem 15.1]
Let
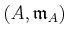 be a regular local ring.
Let
be a regular local ring.
Let
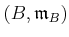 be a Cohen-Macaulay local ring.
Let
be a Cohen-Macaulay local ring.
Let
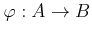 be a local ring homomorphism.We set
be a local ring homomorphism.We set
for the fiber ring of 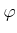 over
over
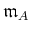 .
Then an equality
.
Then an equality
holds if and only if 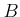 is flat over
is flat over 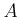 .
.
**



Next: Bibliography
2011-04-14
 is an additive group with respect to the addition.
is an additive group with respect to the addition.
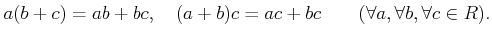
 has a multiplicative unit.
has a multiplicative unit.
![]() , we denote by
, we denote by ![]() (respectively,
(respectively, ![]() )
the zero element of
)
the zero element of ![]() (respectively, the unit element of
(respectively, the unit element of ![]() ).
Namely,
).
Namely, ![]() and
and ![]() are elements of
are elements of ![]() characterized by
the following rules.
characterized by
the following rules.
![]() to
to ![]() is denoted by
is denoted by
![]() . It has an structure of an module in an obvious manner.
Furthermore, when
. It has an structure of an module in an obvious manner.
Furthermore, when ![]() is a commutative ring, then it has a structure of
an
is a commutative ring, then it has a structure of
an ![]() -module.
-module.
![]() -submodule
-submodule ![]() of an
of an ![]() -module
-module ![]() , we have the
following exact sequence.
, we have the
following exact sequence.