


Next: About this document ...
Commutative algebra
Yoshifumi Tsuchimoto

DEFINITION 05.1
Let
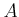
be a ring. Let
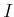
be an ideal of
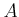
.
The
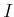
-adic topology on
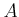
is a topology defined by introducing
for each
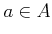
,
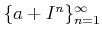
as the neighbourhood base.
It is easy to see that the 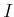 -adic topology is given by a quasi-metric
defined by
-adic topology is given by a quasi-metric
defined by
EXAMPLE 05.3
Let
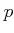
be a prime number. The ring
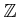
of rational integers equipped
with the
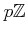
-adic topology is Hausdorff. Its completion is denoted by
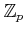
and is called the ring of
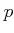
-adic integers.
DEFINITION 05.4
Let
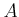
be a ring. Let
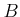
be an
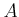
-algebra.
Let
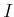
be an ideal of
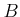
.
We equip
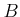
with the
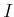
-adic topology.
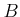
is
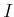 -smooth
-smooth over
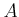
if
for any
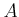
-algebra
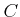
, any ideal
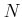
of
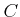
satisfying
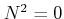
and
any
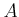
-algebra homomorphism
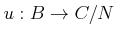
which is continuous
with respect to the discrete topology of
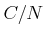
,
there exists a lifting
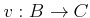
of
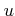
to
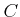
, as an
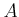
-algebra homormophism.
DEFINITION 05.5
Let
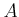
be a ring. Let
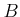
be an
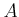
-algebra.
Let
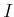
be an ideal of
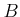
.
We equip
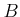
with the
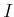
-adic topology.
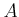
-algebra
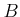
is
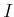 -unramified
-unramified over
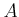
if
for any
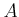
-algebra
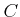
, any ideal
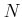
of
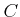
satisfying
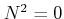
and
any
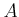
-algebra homomorphism
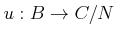
which is continuous
with respect to the discrete topology of
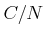
,
there is at most one
lifting
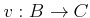
of
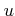
to
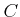
, as an
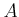
-algebra homormophism.
DEFINITION 05.6
An
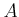
-algebra
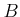
is
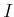
-étale over
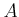
if it is both
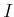
-smooth
and
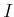
-unramified.
Note that the conditions 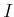 -smooth/unramified/étale become
weaker if we take
-smooth/unramified/étale become
weaker if we take 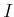 larger.
larger.
In the ``strongest'' case where 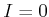 , the continuity of the
homomorphism
, the continuity of the
homomorphism 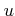 is automatic (any homomorphism is continuous.)
0
-smoothness
(respectively, 0
-unramifiedness, respectively, 0
-étale-ness)
is also refered to as
formal smoothness
(respectively, formal unramifiedness, respectively, formal étale-ness).
is automatic (any homomorphism is continuous.)
0
-smoothness
(respectively, 0
-unramifiedness, respectively, 0
-étale-ness)
is also refered to as
formal smoothness
(respectively, formal unramifiedness, respectively, formal étale-ness).



Next: About this document ...
2011-06-24
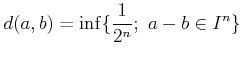
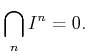
![]() -smooth/unramified/étale become
weaker if we take
-smooth/unramified/étale become
weaker if we take ![]() larger.
larger.
![]() , the continuity of the
homomorphism
, the continuity of the
homomorphism ![]() is automatic (any homomorphism is continuous.)
0
-smoothness
(respectively, 0
-unramifiedness, respectively, 0
-étale-ness)
is also refered to as
formal smoothness
(respectively, formal unramifiedness, respectively, formal étale-ness).
is automatic (any homomorphism is continuous.)
0
-smoothness
(respectively, 0
-unramifiedness, respectively, 0
-étale-ness)
is also refered to as
formal smoothness
(respectively, formal unramifiedness, respectively, formal étale-ness).