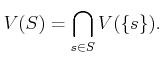Next: About this document ...
Commutative algebra
Yoshifumi Tsuchimoto

DEFINITION 06.1
Let
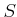
be a ring which contains a subring
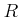
.
An element
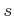
of
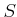
is said to be
integral over
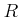
if it is a
root of a monic polynomial in
![$ R[X]$](img5.png)
.
EXAMPLE 06.4
Each element of
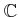
which is integral over
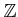
is said to
be an
algebraic integer. The set of algebraic integers forms a
subring of
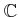
.
DEFINITION 06.5
Let
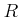
be an integral domain. Let us denote its field of quotients by
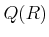
.
The integral closure of
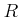
in
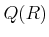
is called the
normalization
of
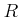
.
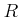
is called
normal if it is equal to its normalizaiton.
By using the Gauss's lemma, we see that every PID is normal.
Normalizations are useful to reduce singularities.
EXAMPLE 06.6
Let us put
and denote the class of
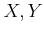
in
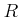
by
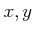
respectively.
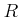
is not normal. Indeed,
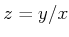
satisfies a monic equation
Thus the normalization
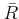
of
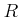
contains the element
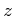
.
Now, let us note that equation
holds so that
![$ R[z]= \mathbb{C}[z]$](img19.png)
holds.
Since
![$ \mathbb{C}[z]$](img20.png)
is normal, we see that
![$ \bar R= R[z]= \mathbb{C}[z]$](img21.png)
.
Note that
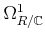
is not locally free whereas
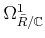
is free.
EXAMPLE 06.7
Let us consider a ring
![$ R=\mathbb{Z}[X]/(u(X))$](img24.png)
where
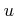
is a monic element
in
![$ \mathbb{Z}[X]$](img26.png)
. Let us denote by
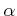
the residue class of
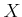
in
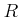
.
EXERCISE 06.1
The normalization of
![% latex2html id marker 1072
$ R=\mathbb{Z}[\sqrt{-3}]$](img30.png)
is equal to
![% latex2html id marker 1074
$ \bar R=\mathbb{Z}[\sqrt{-3}]$](img31.png)
.
Compute
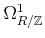
and
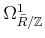
.
**
In other words, a normalization of a ring 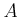 can never be flat
(unless the trivial case where
can never be flat
(unless the trivial case where 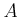 itself is normal).
itself is normal).
**
DEFINITION 06.9
For any commutative ring
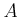
, we define its
spectrum as
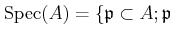
is a prime ideal of $A$
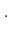
For any subset
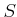
of
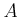
we define
Then we may topologize
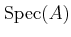
in such a way that the closed
sets are sets of the form
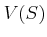
for some
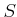
. Namely,
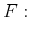
closed
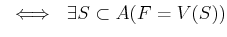
We refer to the topology as the
Zariski topology.
PROPOSITION 06.11
For any ring homomorphism
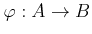 , we have a map
, we have a map
It is continuous with respect to the Zariski topology.



Next: About this document ...
2011-06-09
![]() can never be flat
(unless the trivial case where
can never be flat
(unless the trivial case where ![]() itself is normal).
itself is normal).