実数の集合の例、上限、上界

定義 1.2   実数 $a,b$ について、閉区間 $[a,b]$ と開区間 $(a,b)$ を つぎの式で定める。

$$[a,b] =\{x \in \mbox{${\mathbb{R}}$} \vert a\leq x \leq b\}$$

$$(a,b) =\{x \in \mbox{${\mathbb{R}}$} \vert a < x < b\}$$

◎ $[a,b]$ には端点があって、そこでのようすは $[a,b]$ のほかの点の ようすと大きく異っている。それに対して、$(a,b)$ の各点はどの点も似ている。

◎ $[a,b]$ には最大元があるが、$(a,b)$ にはない。 次の定義を見よ。

定義 1.3   $\mbox{${\mathbb{R}}$}$ の部分集合 $A$ が与えられているとする。 このとき

1. $a\in$   $\mbox{${\mathbb{R}}$}$ が $A$ の上界 (upper bound)であるとは、
   $$\forall x\in A (x\leq a)$$
   (つまり、どの $x\in A$ をもってきても $x\leq a$ ) が成り立つときに言う。
2. $a\in$   $\mbox{${\mathbb{R}}$}$ が $A$ の上限(supremum)であるとは、 $A$ の上界のうち最小のものをいう。

◎ 集合の上界は存在するとは限らない。 また、上界が存在したとすると、それはいくつもある。

例 1.4  

$$T=\{$$土佐電鉄(*)の運賃$$\}=\{100,180,190,260,340,380,400,440,470,500\}$$

とおく((*)2011/4/1現在)。このとき、

1. $T$ の上界としては、$1000$ がある。これは 「土佐電鉄に乗るときは1000円あればひとり分のお金は足りる」ことを 意味している。
2. $T$ の上界としては、他にも 500, 一万、十万、$951.777..$ 等がある。
3. $T$ の上限は $500$ である。

旅行に行くとき、かかる旅費をキッチリ計算して、その分のお金しか 持って行かない人は少なかろう。「大体△万円あれば十分」とか 見積もる。これが上界の考え方。

例 1.5 (最大値を持たないが上限を持つ集合たち)  

1. $\{\frac{n-1}{n}; n=1,2,3,\dots\}$ は上限 $1$ をもつ。
2. $\{x\in$   $\mbox{${\mathbb{R}}$}$$; x<2\}$ は上限 $2$ を持つ。
3. $\{x\in$   $\mbox{${\mathbb{Q}}$}$$; x^2<2\}$ は上限 $\sqrt{2}$ を持つ。

定義 1.6   集合 $A\subset$   $\mbox{${\mathbb{R}}$}$ が上に有界であるとは、 $A$ が上界を少なくとも一つもつときに言う。

例題 1.7   $f(x)=x^4-6 x^3 +11 x^2 -6 x$ とおく。このとき

$$S=\{ x\in$$   $$\mbox{${\mathbb{R}}$}$$$$; f(x) <0\}$$

は上界をもつだろうか、

(解答) $f(x)=x(x-1)(x-2)(x-3)$ と因数分解できるので、

$$S=(0,1) \cup (2,3)$$

であることがわかる。 したがって、 $S$ は上界 $10$ をもち、上に有界である。

上界は一つ挙げれば十分である。上の例題なら $3$ (上限) でも良いし、 $100$ でもよい。$f$ が因数分解できない場合も、 つぎのような別解ならうまくいく。

(別解) まず、$M=100$ とおくと、$S$ の元 $s$ は $s\leq M$ を満たす。 なぜなら、もし $s>M$ なる $s\in S$ が存在したとすると、

$$f(s) = s^4-6 s^3 +11 s^2 - 6 s$$

$$> 100 s^3 -6 s^3 + 11 \cdot 0 - 6 \cdot s^3 = 88 s^3 >0$$

となって、これは $s\in S$ に反するからである。 ($s>1$ のとき $s<s^2<s^3<\dots$ に注意。 負の項は多めに見積もり、正の項は控えめに見積もる。) したがって、 $M$ は $S$ の上界の一つである。

定義 1.8   実数 $x$ に対して、その絶対値 $\vert x\vert$ を次のように定義する。

$$\vert x\vert= \sqrt{x^2} = \begin{cases}\phantom{-} x & \text{ if } x\geq 0 -x & \text{ if } x< 0 \end{cases}$$

(ただし平方根は0以上のほうを選ぶ。)

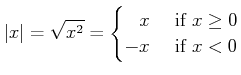上の平方根を使う定義は次のように 高次元の空間にも容易に拡張できるという長所を持つ。

$$\vert\vert(x_1,x_2,\dots,x_n)\vert\vert=\sqrt{x_1^2+x_2^2+x_3^2+\dots + x_n^2}$$

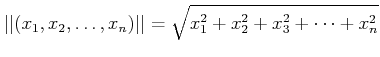
次に出てくる三角不等式も実は高次元の場合にも成り立ち、 解析学の基本的な道具として大切である。

定理 1.9   次の不等式が成り立つ。

1. $x\in$   $\mbox{${\mathbb{R}}$}$ に対して、 $-\vert x\vert \leq x \leq \vert x\vert$ .
2. (三角不等式) $x,y\in$   $\mbox{${\mathbb{R}}$}$ に対して、 $\vert x+y\vert \leq \vert x\vert+\vert y\vert.$

問題 1.1  

$$S=\{ x\in$$   $$\mbox{${\mathbb{R}}$}$$$$; 5x^4-4 x^3+3 x^2+4 x -5<0\}$$

は上界をもつだろうか、 もつ場合には上界を一つ挙げてその理由を説明し、 もたない場合にはもたないことの理由を説明せよ。