


Next: About this document ...
微分積分学概論AI要約 No.2
第2回目の主題 :

次の公理は実数の基本的な性質である。
公理 2.1
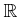
の部分集合
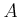
が上に有界ならば、
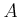
は上限を持つ。
定義 2.2
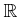
の部分集合
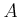
に対して、その上限のことを
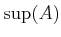
と書く。
補題 2.3
集合
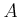
の上限が
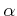
であることは、次の二条件が同時に成り立つことと
同値である。
-
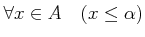 .
.
-
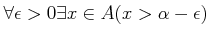 .
.
「
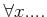 」
は、「どんな
」
は、「どんな 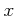 に対しても、
に対しても、 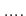 がなりたつ」という意味、
がなりたつ」という意味、
「
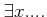 」
は、「なにかある一つの
」
は、「なにかある一つの 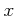 に対しては、
に対しては、 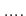 がなりたつ」という意味で用いる。
がなりたつ」という意味で用いる。
正の整数の全体のことをこの講義では
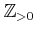 と書く。
数列とは、数学的には次のように定義できる。
と書く。
数列とは、数学的には次のように定義できる。
定義 2.4
実数列
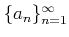
とは、
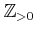
から
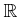
への写像
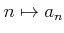
(すなわち、正の整数
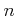
に実数
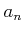
を対応させる対応)のことである。
数列 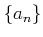 を単なる集合と見てそれが有界かどうか、や
その上限
を単なる集合と見てそれが有界かどうか、や
その上限 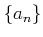 を議論することができる。公理 2.1により、
上に有界な数列は
上限を持つことがわかる。
を議論することができる。公理 2.1により、
上に有界な数列は
上限を持つことがわかる。
定義 2.5
実数列
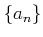
が
単調増加であるとは、
がなりたつときにいう。
もっと露骨に言えば 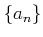 が単調増加であるとは
が単調増加であるとは
が成り立つということである。
補題 2.6
数列
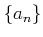
を
で定義する。このとき
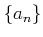 は単調増加である。
は単調増加である。
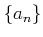 は有界である。
は有界である。
定義 2.7
上限
のことを
自然対数の底とよび、
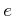
と書く。
問題 2.1
正の実数
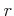
をひとつ固定したとき、
で定義される数列
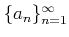
は上に有界であることを示しなさい。
参考のために、
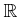 の性質で必要最小限のものを書いておこう。
の性質で必要最小限のものを書いておこう。
よく知っている体
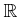 から少し離れて、次のような集合
から少し離れて、次のような集合 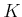 (とその上の演算
(とその上の演算 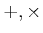 ,元
,元 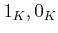 ,関係式
,関係式 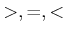 )を考える。
)を考える。
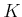 は体である。すなわち:
は体である。すなわち:
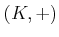 は加法群である。
は加法群である。
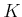 の各元
の各元 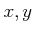 に対して、その和と呼ばれる元
に対して、その和と呼ばれる元 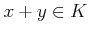 が
ただひとつ定まる。
が
ただひとつ定まる。
-
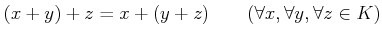 .
.
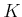 にはゼロ元
にはゼロ元 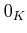 と呼ばれる元が存在して、
任意の
と呼ばれる元が存在して、
任意の 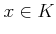 に対して
に対して
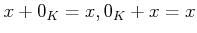 を満たす。
を満たす。
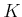 の各元
の各元 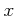 に対して、そのマイナス元
に対して、そのマイナス元 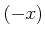 と呼ばれる元が
存在して、
と呼ばれる元が
存在して、
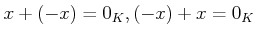 を満たす。
を満たす。
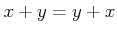 .
.
-
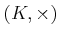 は乗法に関して半群をなす。すなわち、
は乗法に関して半群をなす。すなわち、
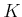 の各元
の各元 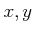 に対して、その積と呼ばれる元
に対して、その積と呼ばれる元 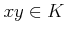 が
ただひとつ定まる。
が
ただひとつ定まる。
-
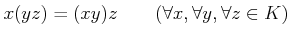 .
.
- 分配法則。
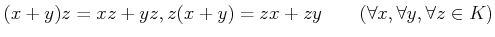 .
.
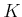 は乗法に関する単位元
は乗法に関する単位元 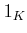 をもつ。すなわち、
任意の
をもつ。すなわち、
任意の 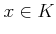 に対して
に対して
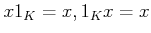 を満たす。
を満たす。
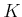 の乗法は可換である。
の乗法は可換である。
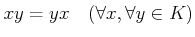 .
.
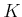 の
の 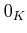 以外の元
以外の元 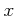 は乗法に関して逆元
は乗法に関して逆元 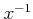 と呼ばれる元が存在して、
と呼ばれる元が存在して、
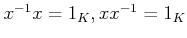 を満たす。
を満たす。
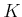 は全順序集合である。
は全順序集合である。
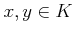 に対して、
に対して、 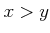 か
か 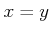 か
か 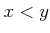 のいずれかが成り立つ。
のいずれかが成り立つ。
-
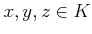 にたいして、「(
にたいして、「(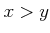 and
and 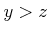 ) ならば
) ならば 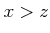 」が成り立つ。
」が成り立つ。
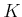 の体の構造と順序構造は両立する。
の体の構造と順序構造は両立する。
-
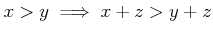 .
.
-
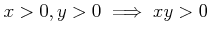 .
.
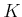 の任意の有界部分集合は
の任意の有界部分集合は 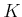 内に上限を持つ。
内に上限を持つ。
このとき、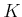 は実数体
は実数体
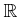 と「同じ」(順序体として同型)である。
と「同じ」(順序体として同型)である。
群、加法群、体について、その詳しい性質は2年生からの代数学で深く勉強する。



Next: About this document ...
2011-04-15
![]()
![]() 」
は、「どんな
」
は、「どんな ![]() に対しても、
に対しても、 ![]() がなりたつ」という意味、
がなりたつ」という意味、
![]() 」
は、「なにかある一つの
」
は、「なにかある一つの ![]() に対しては、
に対しては、 ![]() がなりたつ」という意味で用いる。
がなりたつ」という意味で用いる。
![]() と書く。
数列とは、数学的には次のように定義できる。
と書く。
数列とは、数学的には次のように定義できる。
![]() を単なる集合と見てそれが有界かどうか、や
その上限
を単なる集合と見てそれが有界かどうか、や
その上限 ![]() を議論することができる。公理 2.1により、
上に有界な数列は
上限を持つことがわかる。
を議論することができる。公理 2.1により、
上に有界な数列は
上限を持つことがわかる。
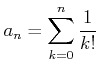
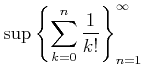
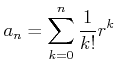
![]() の性質で必要最小限のものを書いておこう。
の性質で必要最小限のものを書いておこう。
![]() から少し離れて、次のような集合
から少し離れて、次のような集合 ![]() (とその上の演算
(とその上の演算 ![]() ,元
,元 ![]() ,関係式
,関係式 ![]() )を考える。
)を考える。
![]() は実数体
は実数体
![]() と「同じ」(順序体として同型)である。
と「同じ」(順序体として同型)である。